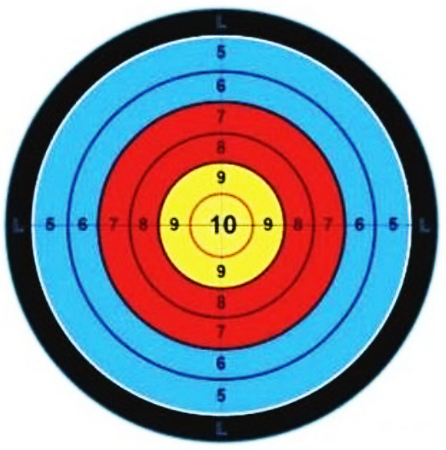
Một xạ thủ bắn bia, trên bia có các vòng tròn tính điểm (từ \(5\) đến \(10\)) như hình vẽ. Mỗi lần bắn, xác suất xạ thủ bắn trúng vòng \(8\) là \(0,25\); trúng vòng dưới 8 (kể cả bắn trượt) là \(0,4\). Gọi \({P_1},{P_2}\) lần lượt là xác suất xạ thủ đó bắn trúng vòng \(10\) và vòng \(9\) trong mỗi lần bắn. Biết rằng nếu xạ thủ đó bắn ba phát vào bia thì xác suất cả ba lần bắn trúng vòng \(10\) là \(0,003375\).
a) \({P_1} = 0,15\).
Một xạ thủ bắn bia, trên bia có các vòng tròn tính điểm (từ \(5\) đến \(10\)) như hình vẽ. Mỗi lần bắn, xác suất xạ thủ bắn trúng vòng \(8\) là \(0,25\); trúng vòng dưới 8 (kể cả bắn trượt) là \(0,4\). Gọi \({P_1},{P_2}\) lần lượt là xác suất xạ thủ đó bắn trúng vòng \(10\) và vòng \(9\) trong mỗi lần bắn. Biết rằng nếu xạ thủ đó bắn ba phát vào bia thì xác suất cả ba lần bắn trúng vòng \(10\) là \(0,003375\).

a) \({P_1} = 0,15\).
Quảng cáo
Trả lời:
Theo bài ra, ta có bảng sau:
a) Đúng. Xác suất cả ba lần bắn trúng vòng \(10\) là: \({\left( {{P_1}} \right)^3} = 0,003375 \Rightarrow {P_1} = \sqrt[3]{{0,003375}} = 0,15\).
Câu hỏi cùng đoạn
Câu 2:
b) \({P_2} = 0,18\).
b) \({P_2} = 0,18\).
b) Sai. Ta có \({P_1} + {P_2} + 0,25 + 0,4 = 1 \Rightarrow {P_2} = 1 - \left( {{P_1} + 0,25 + 0,4} \right) = 1 - \left( {0,15 + 0,25 + 0,4} \right) = 0,2\).
Câu 3:
c) Nếu xạ thủ đó bắn ba phát thì xác suất đạt \(29\) điểm là \(0,0045\).
c) Sai. Ta có \(29 = 9 + 10 + 10\). Xảy ra các trường hợp như sau:
Do đó, xác suất bắn \(3\) lần đạt \(29\) điểm là \[3 \times 0,2 \times {\left( {0,15} \right)^2} = 0,0135\].
Câu 4:
d) Nếu xạ thủ đó bắn ba phát thì xác suất đạt ít nhất \(28\) điểm là \(0,05175\).
d) Nếu xạ thủ đó bắn ba phát thì xác suất đạt ít nhất \(28\) điểm là \(0,05175\).
d) Đúng. Xác suất đạt ít nhất \(28\) điểm sau \(3\) lần bắn.
TH1: Xác suất đạt \(30\) điểm là \(P\left( {{d_1}} \right) = {\left( {0,15} \right)^3} = 0,003375\).
TH2: Xác suất đạt \(29\) điểm là \(P\left( {{d_2}} \right) = 3 \cdot {\left( {0,15} \right)^2} \cdot 0,2 = 0,0135\).
TH3: Xác suất đạt \(28\) điểm.
Ta có \(28 = 10 + 10 + 8 = 9 + 9 + 10\).
Þ Xác suất đạt \(28\) điểm là \(P\left( {{d_3}} \right) = 3 \times 0,25 \times {\left( {0,15} \right)^2} + 3 \times 0,15 \times {\left( {0,2} \right)^2} = 0,034875\)
Do đó, xác suất đạt ít nhất 28 điểm sau \(3\) lần bắn là
\(P = P\left( {{d_1}} \right) + P\left( {{d_2}} \right) + P\left( {{d_3}} \right) = 0,003375 + 0,0135 + 0,034875 = 0,05175\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 2,07.
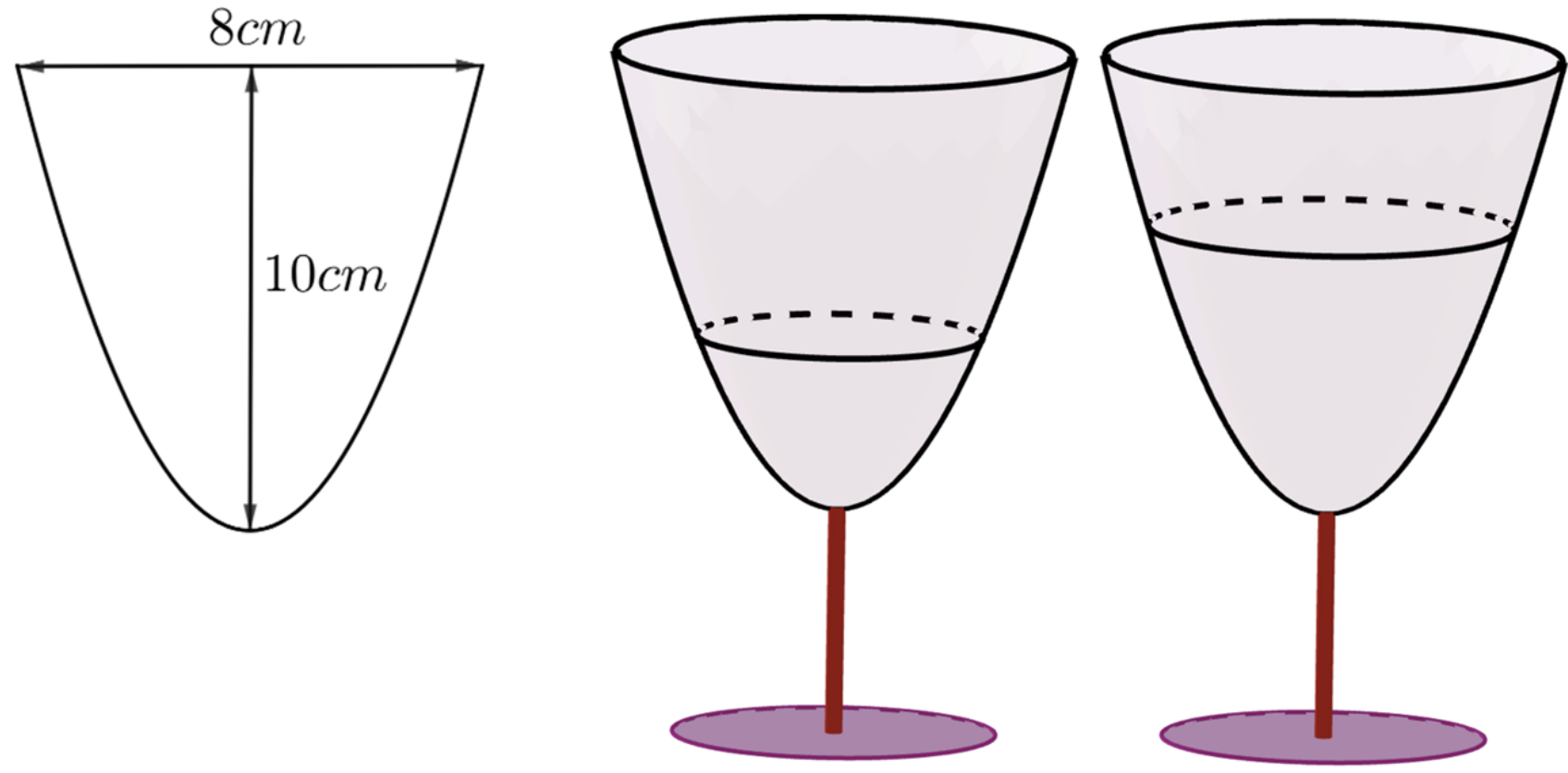
Chọn hệ trục tọa độ Oxy như hình vẽ dưới đây:
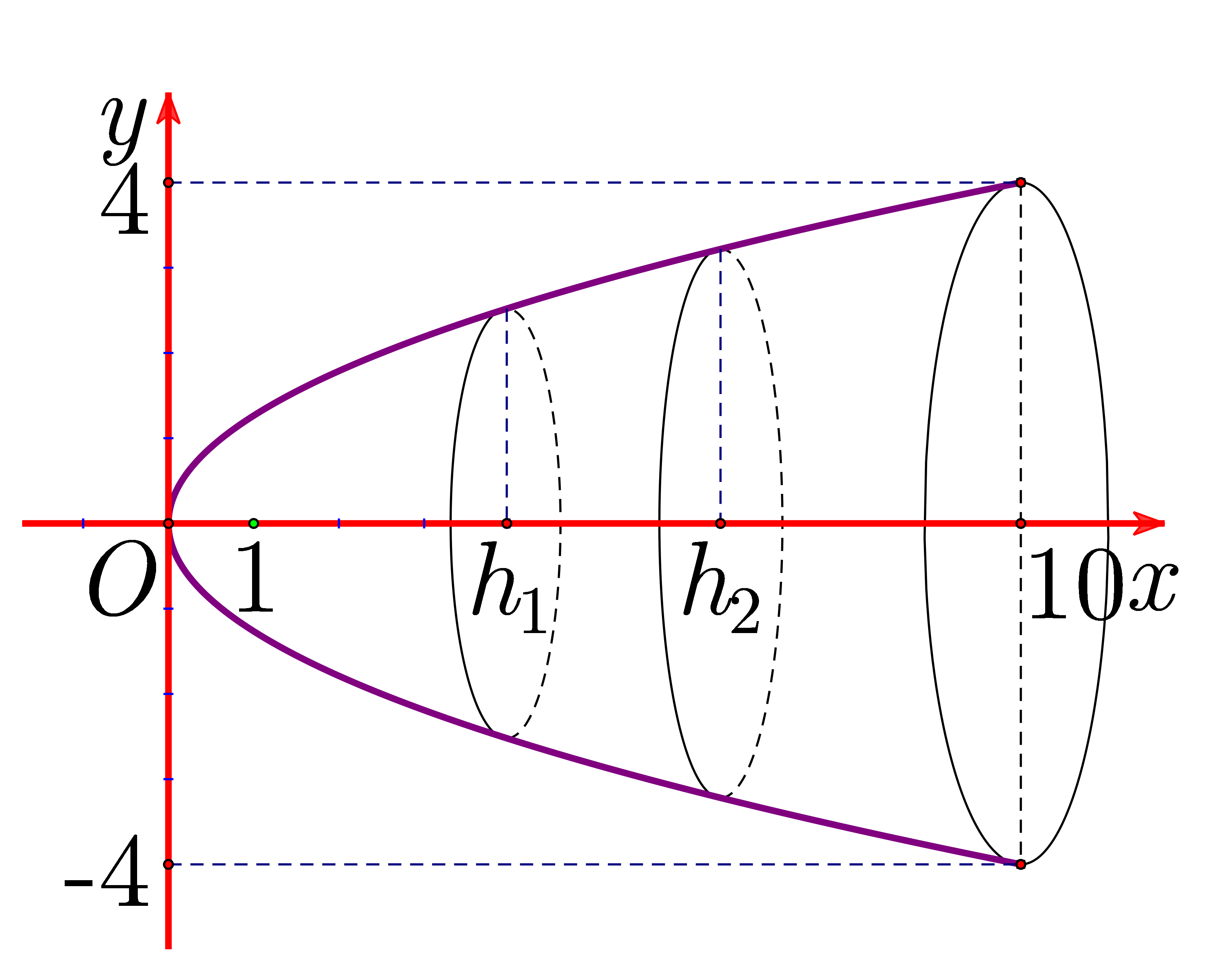
Gọi dạng của parabol là \(\left( P \right):{y^2} = 2px\).
Ta có \(x = 10,y = 4 \Rightarrow p = \frac{4}{5} \Rightarrow \left( P \right):{y^2} = \frac{8}{5}x\).
Thể tích ly nước nếu đổ đầy: \(V = \pi \int\limits_0^{10} {{y^2}{\rm{d}}x} = \pi \int\limits_0^{10} {\frac{8}{5}x{\rm{d}}x} = \left. {\frac{{4\pi {x^2}}}{5}} \right|_0^{10} = 80\pi .\)
Thể tích của nước trong ly lúc mới đổ lần đầu là: \(\pi \int\limits_0^{{h_1}} {\frac{8}{5}x{\rm{d}}x} = \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_1^2}}{5} = 20 \Rightarrow {h_1} = 5\).
Khi đó, chiều cao của nước ban đầu là \({h_1} = 5\,\left( {{\rm{cm}}} \right)\).
Thể tích của nước trong ly sau khi đổ thêm là: \(\pi \int\limits_0^{{h_2}} {\frac{8}{5}x{\rm{d}}x} = 2 \cdot \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_2^2}}{5} = 40 \Rightarrow {h_2} = 5\sqrt 2 \).
Chiều cao của mực nước sau khi đổ thêm là \({h_2} = 5\sqrt 2 \,\,\left( {{\rm{cm}}} \right)\).
Chiều cao của mực nước tăng thêm so với ban đầu: \(h = {h_2} - {h_1} = 5\sqrt 2 - 5 \approx 2,07{\rm{ (cm)}}{\rm{.}}\)
Lời giải
Đáp án: \(0,5\).
Gọi \(A\) là biến cố: “Trong 3 viên bi lấy ra từ hộp hai có 2 viên bi từ hộp thứ nhất chuyển sang”.
Gọi \(B\) là biến cố: “Ba viên bi lấy ra từ hộp hai là màu trắng”.
Trường hợp 1: 2 viên bi từ hộp thứ nhất chuyển sang là 2 viên bi trắng. Khi đó:
\({P_1}\left( B \right) = \frac{{C_7^2}}{{C_{12}^2}} \cdot \frac{{C_6^3}}{{C_{12}^3}} = \frac{7}{{242}}\).
Trường hợp 2: 2 viên bi từ hộp thứ nhất chuyển sang là 2 viên bi đỏ. Khi đó:
\({P_2}\left( B \right) = \frac{{C_5^2}}{{C_{12}^2}} \cdot \frac{{C_4^3}}{{C_{12}^3}} = \frac{1}{{363}}\).
Trường hợp 3: 2 viên bi từ hộp thứ nhất chuyển sang là 1 viên bi trắng và 1 viên bi đỏ. Khi đó:
\({P_3}\left( B \right) = \frac{{C_7^1.C_5^1}}{{C_{12}^2}} \cdot \frac{{C_5^3}}{{C_{12}^3}} = \frac{{35}}{{1452}}\).
Suy ra \(P\left( B \right) = {P_1}\left( B \right) + {P_2}\left( B \right) + {P_3}\left( B \right) = \frac{{27}}{{284}}\) và \(P\left( {AB} \right) = {P_1}\left( B \right) = \frac{7}{{242}}\).
Do đó, \(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{\frac{7}{{242}}}}{{\frac{{27}}{{484}}}} = \frac{{14}}{{27}} \approx 0,5\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.