PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
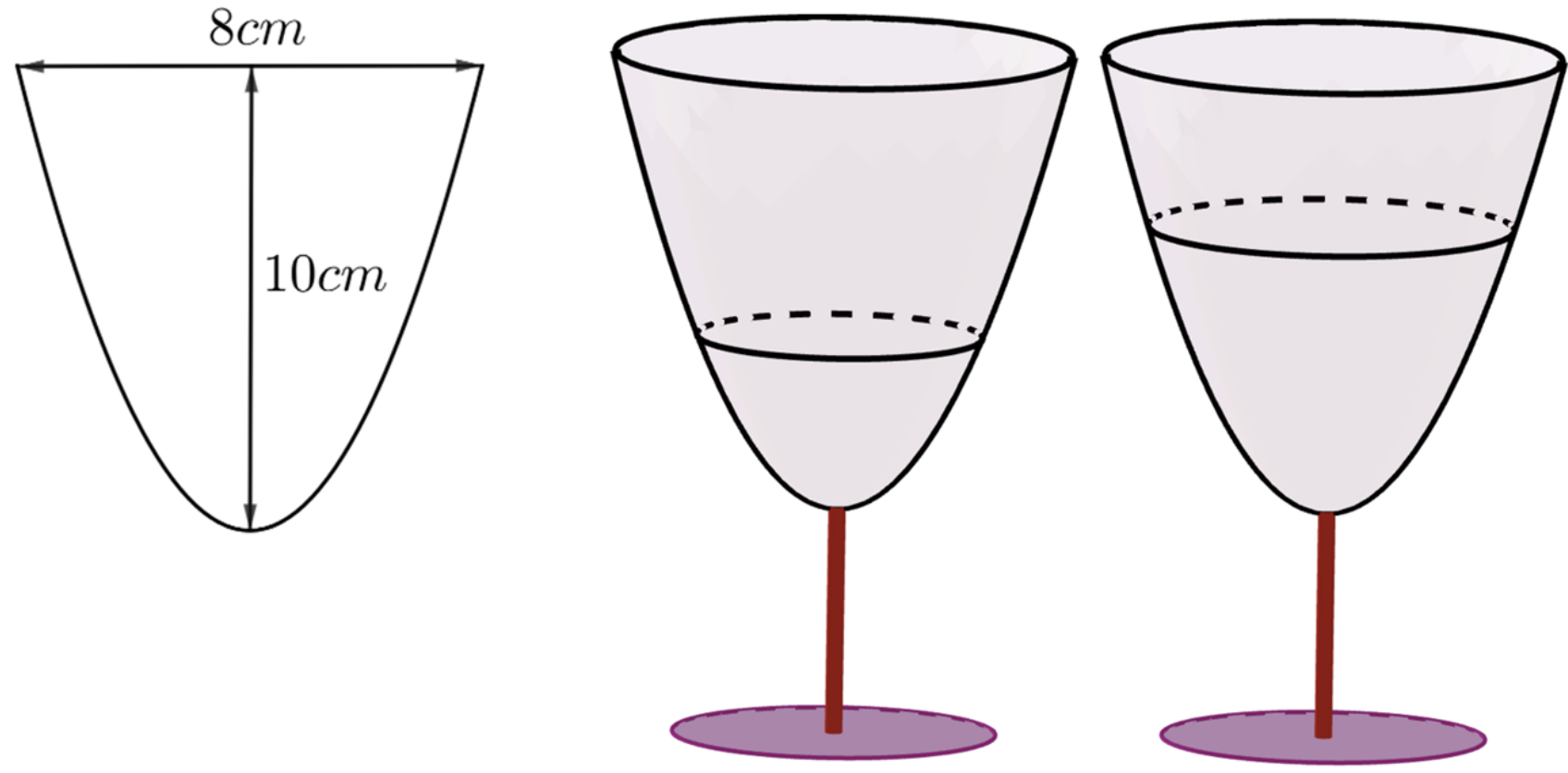
Chi phí về nhiên liệu của một con tàu được chia làm hai phần. Phần chi phí thứ nhất không phụ thuộc vào tốc độ tàu và bằng 480 nghìn đồng mỗi giờ. Chi phí phần thứ hai trên 1 km đường tỉ lệ thuận với lập phương của tốc độ tàu, khi tốc độ bằng \(20\)km/h thì chi phí phần thứ hai bằng 100 nghìn đồng mỗi giờ. Giả sử con tàu đó luôn giữ nguyên tốc độ di chuyển, để tổng chi phí nhiên liệu trên 1 km đường là nhỏ nhất thì tốc độ của con tàu đó bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần chục).
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Chi phí về nhiên liệu của một con tàu được chia làm hai phần. Phần chi phí thứ nhất không phụ thuộc vào tốc độ tàu và bằng 480 nghìn đồng mỗi giờ. Chi phí phần thứ hai trên 1 km đường tỉ lệ thuận với lập phương của tốc độ tàu, khi tốc độ bằng \(20\)km/h thì chi phí phần thứ hai bằng 100 nghìn đồng mỗi giờ. Giả sử con tàu đó luôn giữ nguyên tốc độ di chuyển, để tổng chi phí nhiên liệu trên 1 km đường là nhỏ nhất thì tốc độ của con tàu đó bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần chục).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(22,5\).
Gọi \(x\,\,{\rm{(km/h)}}\) là tốc độ của tàu.
Thời gian tàu chạy quãng đường 1 km là \(\frac{1}{x}\) (giờ).
Chi phí tiền nhiên liệu phần thứ nhất cho quãng đường 1 km là: \(\frac{1}{x} \cdot 480\) (nghìn đồng).
Gọi \(y\) (nghìn đồng) là chi phí nhiên liệu phần thứ hai cho quãng đường 1 km ứng với tốc độ \(x\). Ta có \(y\) tỉ lệ thuận với lập phương tốc độ nên \(y = k{x^3}\) với \(k > 0\).
Khi tốc độ \(x = 20\,\,{\rm{(km/h)}}\) thì thời gian tàu chạy 1 km là \(\frac{1}{{20}}\) (giờ) nên chi phí phần thứ 2 cho quãng đường 1 km là \(\frac{1}{{20}} \cdot 100 = 5\) (nghìn đồng).
Suy ra \(5 = k \cdot {20^3}\) nên \(k = \frac{5}{{{{20}^3}}} = \frac{1}{{1600}}\), do đó \(y = \frac{{{x^3}}}{{1600}}\).
Vậy tổng chi phí tiền nhiên liệu cho 1 km đường là: \(P\left( x \right) = \frac{{480}}{x} + \frac{{{x^3}}}{{1600}}\).
Bài toán trở thành tìm \(x\) để \(P\left( x \right)\) nhỏ nhất.
Có \(P'\left( x \right) = - \frac{{480}}{{{x^2}}} + \frac{{3{x^2}}}{{1600}};\,\,P'\left( x \right) = 0 \Leftrightarrow \frac{{3{x^2}}}{{1600}} = \frac{{480}}{{{x^2}}} \Rightarrow x = 4\sqrt[4]{{1000}}\).
Lập bảng biến thiên suy ra \(P\left( x \right)\) đạt GTNN tại \(x = 4\sqrt[4]{{1000}}\).
Vậy để tổng chi phí trên 1 km đường nhỏ nhất thì vận tốc của tàu là \(x = 4\sqrt[4]{{1000}} \approx 22,5\,{\rm{(km/h)}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án: 2,07.
Chọn hệ trục tọa độ Oxy như hình vẽ dưới đây:
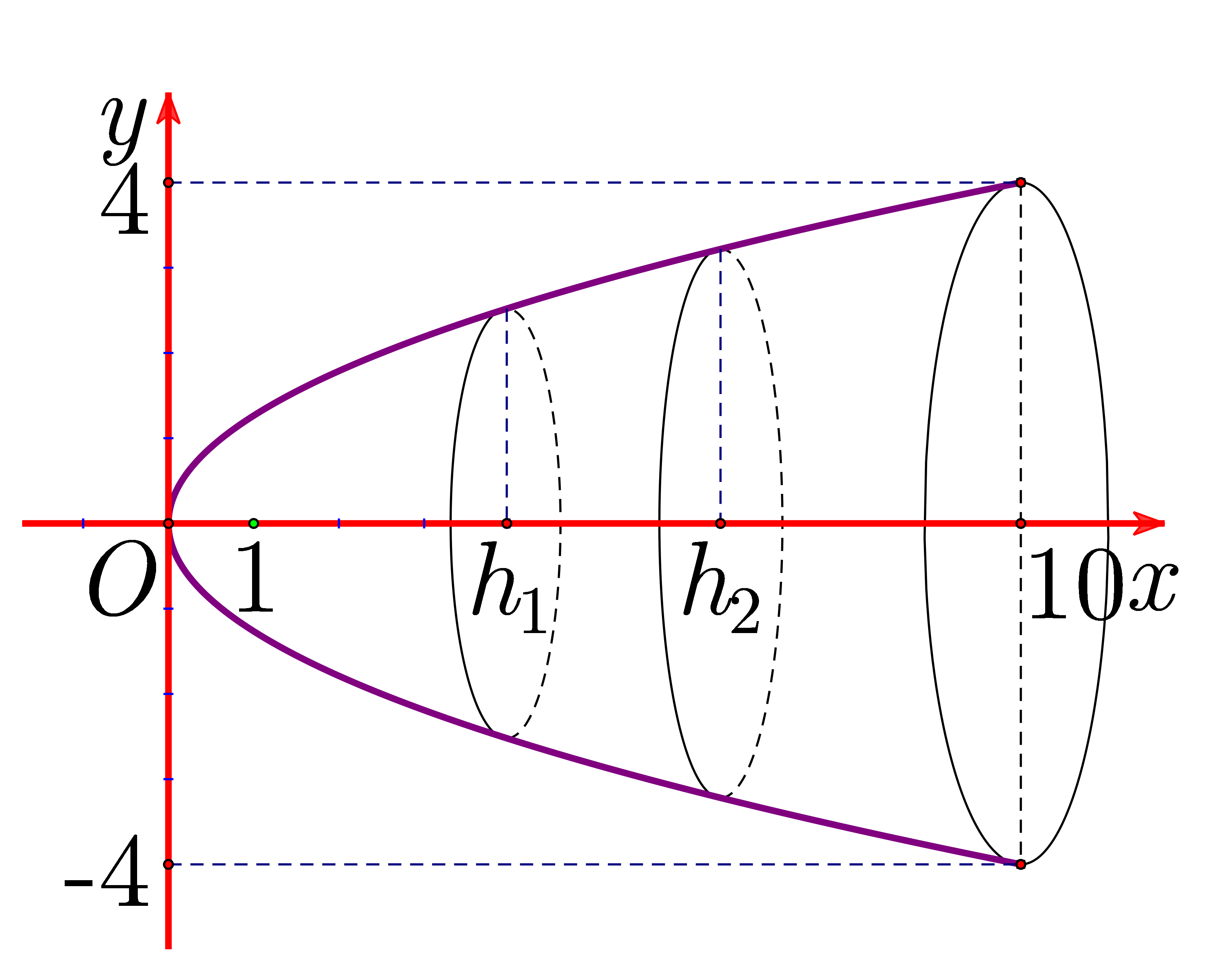
Gọi dạng của parabol là \(\left( P \right):{y^2} = 2px\).
Ta có \(x = 10,y = 4 \Rightarrow p = \frac{4}{5} \Rightarrow \left( P \right):{y^2} = \frac{8}{5}x\).
Thể tích ly nước nếu đổ đầy: \(V = \pi \int\limits_0^{10} {{y^2}{\rm{d}}x} = \pi \int\limits_0^{10} {\frac{8}{5}x{\rm{d}}x} = \left. {\frac{{4\pi {x^2}}}{5}} \right|_0^{10} = 80\pi .\)
Thể tích của nước trong ly lúc mới đổ lần đầu là: \(\pi \int\limits_0^{{h_1}} {\frac{8}{5}x{\rm{d}}x} = \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_1^2}}{5} = 20 \Rightarrow {h_1} = 5\).
Khi đó, chiều cao của nước ban đầu là \({h_1} = 5\,\left( {{\rm{cm}}} \right)\).
Thể tích của nước trong ly sau khi đổ thêm là: \(\pi \int\limits_0^{{h_2}} {\frac{8}{5}x{\rm{d}}x} = 2 \cdot \frac{1}{4} \cdot 80\pi \Leftrightarrow \frac{{4h_2^2}}{5} = 40 \Rightarrow {h_2} = 5\sqrt 2 \).
Chiều cao của mực nước sau khi đổ thêm là \({h_2} = 5\sqrt 2 \,\,\left( {{\rm{cm}}} \right)\).
Chiều cao của mực nước tăng thêm so với ban đầu: \(h = {h_2} - {h_1} = 5\sqrt 2 - 5 \approx 2,07{\rm{ (cm)}}{\rm{.}}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng. Vì các điểm \(E,F\) lần lượt là các điểm chính giữa của các cung nên \(E = \left( { - 4\cos 45^\circ ;4\sin 45^\circ } \right) = \left( { - 2\sqrt 2 ;2\sqrt 2 } \right)\), tương tự \(F\left( {2\sqrt 2 ; - 2\sqrt 2 } \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập