Một công ty vận tải cần giao hàng đến tất cả các thành phố \(A\), \(B\), \(C\), \(D\), \(E\) (hình vẽ). Chi phí di chuyển giữa các thành phố được mô tả trên hình (tính theo đơn vị nghìn đồng). Xe giao hàng của công ty xuất phát từ thành phố \(A\) đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố \(A\). Tìm chi phí thấp nhất của xe giao hàng (tính theo đơn vị nghìn đồng)?
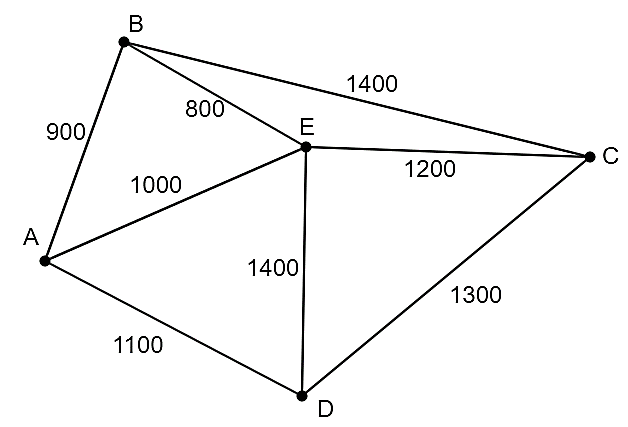
Một công ty vận tải cần giao hàng đến tất cả các thành phố \(A\), \(B\), \(C\), \(D\), \(E\) (hình vẽ). Chi phí di chuyển giữa các thành phố được mô tả trên hình (tính theo đơn vị nghìn đồng). Xe giao hàng của công ty xuất phát từ thành phố \(A\) đi qua tất cả các thành phố còn lại đúng một lần sau đó trở lại thành phố \(A\). Tìm chi phí thấp nhất của xe giao hàng (tính theo đơn vị nghìn đồng)?

Quảng cáo
Trả lời:
Đáp án: 5300.
Cách 1: Liệt kê các đường đi có thể liên thông
Các hành trình có thể và chi phí tương ứng:
1. \(A \to B \to E \to C \to D \to A\): \(900 + 800 + 1200 + 1300 + 1100 = 5300\)
2. \(A \to B \to E \to D \to C \to A\): \(900 + 800 + 1400 + 1300 + 1200 = 5600\)
3. \(A \to B \to C \to E \to D \to A\): \(900 + 1400 + 1200 + 1400 + 1100 = 6000\)
4. \(A \to B \to C \to D \to E \to A\): \(900 + 1400 + 1300 + 1400 + 1000 = 6000\)
5. \(A \to E \to B \to C \to D \to A\): \(1000 + 800 + 1400 + 1300 + 1100 = 5600\)
6. \(A \to E \to D \to C \to B \to A\): \(1000 + 1400 + 1300 + 1400 + 900 = 6000\)
7. \(A \to D \to C \to B \to E \to A\): \(1100 + 1300 + 1400 + 800 + 1000 = 5600\)
8. \(A \to D \to C \to E \to B \to A\): \(1100 + 1300 + 1200 + 800 + 900 = 5300\)
9. \(A \to D \to E \to B \to C \to A\): \(1100 + 1400 + 800 + 1400 + 1200 = 5900\)
10. \(A \to D \to E \to C \to B \to A\): \(1100 + 1400 + 1200 + 1400 + 900 = 6000\)
Kết luận: Chi phí thấp nhất mà xe tải của công ty vận tải phải trả là \(5300\) nghìn đồng, ứng với các hành trình:
1. \(A \to B \to E \to C \to D \to A\)
8. \(A \to D \to C \to E \to B \to A\)
@ Cách 2: Lý thuyết đồ thị
⮚ Hình bên là một đơn đồ thị liên thông có \(5\) đỉnh.
⮚ Do bậc của các đỉnh đều lớn hơn hoặc bằng \(3\) nên đồ thị có chu trình Hamilton.
Chúng ta cần tìm một chu trình Hamilton có tổng trọng số nhỏ nhất trong đồ thị đã cho, bắt đầu và kết thúc tại đỉnh \(A\).
Dùng phương pháp gắn nhãn ta thấy chu trình \(A \to B \to E \to C \to D \to A\) có chi phí thấp nhất là \(5300\) nghìn đồng.
Chu trình ngược lại \(A \to D \to C \to E \to B \to A\) cũng có chi phí tương đương:
\[1100 + 1300 + 1200 + 800 + 900 = 5300\].
Vậy, chi phí thấp nhất mà xe hàng phải trả là \(5300\) nghìn đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 50.
Ta có giá bán cho mỗi tấn sản phẩm là \(p\left( x \right) = 90 - 0,01{x^2}\) (triệu đồng).
Nên bán \(x\) tấn sản phẩm thu được \(\left( {90 - 0,01{x^2}} \right)x\) (triệu đồng). Điều kiện \(0 < x \le 100\).
Lợi nhuận hàng tháng của nhà máy \(A\) khi sản xuất và bán \(x\) tấn sản phẩm cho nhà máy \(B\) là:
\(L\left( x \right) = \left( {90 - 0,01{x^2}} \right)x \cdot 90\% - \frac{1}{2}\left( {200 + 27x} \right)\) (triệu đồng).
Hay \(L\left( x \right) = - 0,009{x^3} + 67,5x - 100\).
Xét hàm số \(L\left( x \right) = - 0,009{x^3} + 67,5x - 100\) trên nửa khoảng \(\left( {0;100} \right]\):
\(L'\left( x \right) = - 0,027{x^2} + 67,5\);
\(L'\left( x \right) = 0 \Leftrightarrow - 0,027{x^2} + 67,5 = 0 \Leftrightarrow {x^2} = 2500 \Rightarrow x = 50\).
Bảng biến thiên:
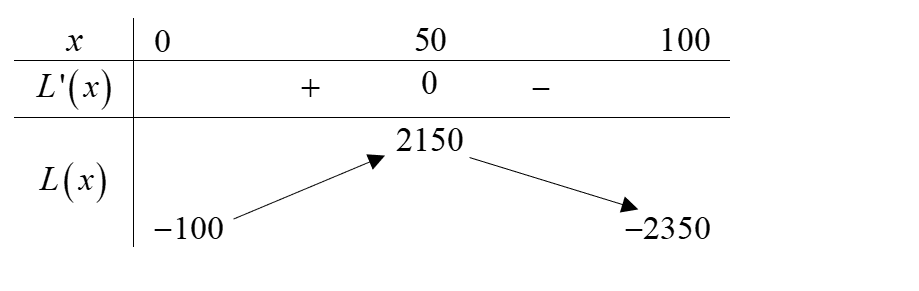
Như vậy nhà máy \(A\) cần sản xuất và bán \(50\) tấn sản phẩm cho nhà máy \(B\) mỗi tháng để thu được lợi nhuận cao nhất.
Lời giải
Đáp án: 711.
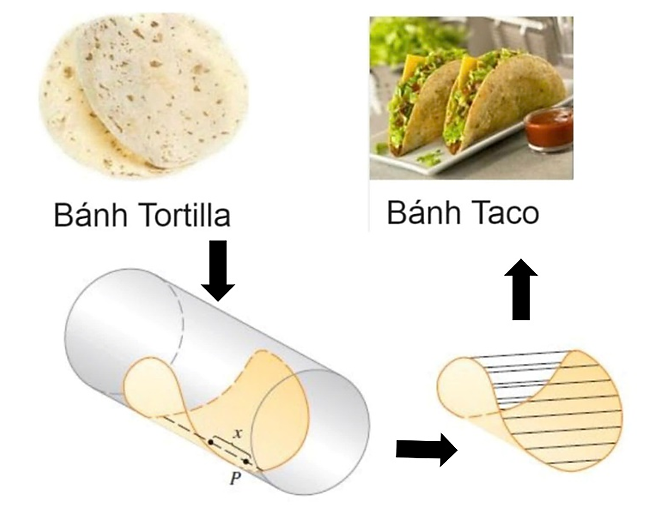
Chu vi của đường tròn có bán kính bằng 4 là \(2 \cdot 4\pi \approx 25,133\).
Như vậy khi trải miếng bánh có đường kính 20 thì còn thừa hai đầu là \(2 \cdot 4\pi - 20 \approx 5,133\).
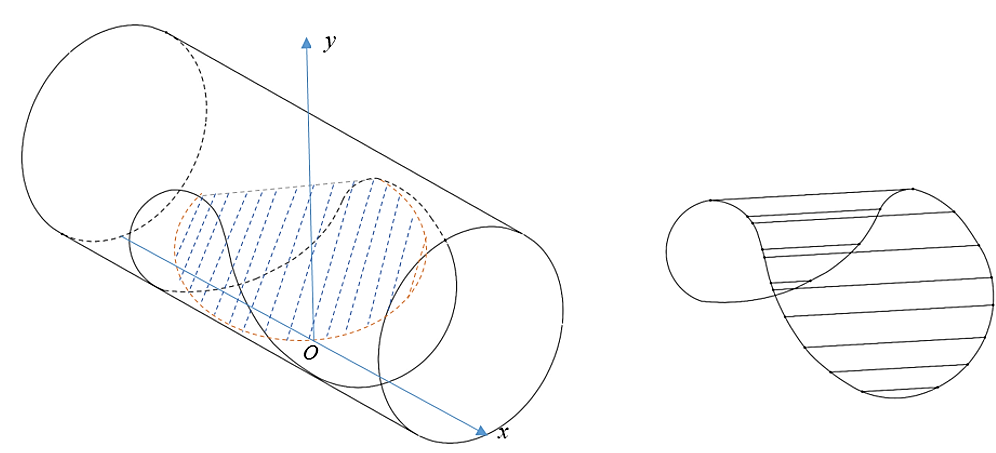
Xét mặt cắt ngang của miếng bánh, mỗi mặt cắt vuông góc với trục tọa độ \(Ox\) là một hình quạt.
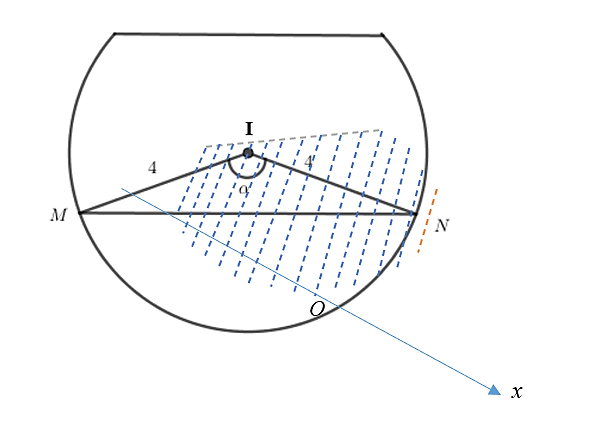
Gọi \(x\,,\, - 10 \le x \le 10\) là hoành độ của mặt phẳng cắt trên. Chọn hệ trục tọa độ như hình vẽ.
Ta có .
Diện tích mặt cắt
\[S\left( x \right) = \frac{{MN}}{2} \cdot R - {S_{\Delta IMN}} = \frac{{2\sqrt {{{10}^2} - {x^2}} \cdot 4}}{2} - \frac{1}{2}{4^2}\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right) = 4\sqrt {{{10}^2} - {x^2}} - 8\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right)\].
Khi đó thể tích chiếc bánh là:
\[V = 2\int\limits_0^{10} {S\left( x \right){\rm{d}}x = } 2\int\limits_0^{10} {\left[ {4\sqrt {{{10}^2} - {x^2}} - 8\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right)} \right]{\rm{d}}x \approx 711\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)} \].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
Thời gian (phút)
\[\left[ {10;15} \right)\]
\[\left[ {15;20} \right)\]
\[\left[ {20;25} \right)\]
\[\left[ {25;30} \right)\]
\[\left[ {30;35} \right)\]
Số ngày tập của Hưng
\[2\]
\[14\]
\[8\]
\[3\]
\[3\]
Số ngày tập của Bình
\[12\]
\[8\]
\[7\]
\[3\]
\[0\]
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của Hưng và Bình lần lượt là
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
|
Thời gian (phút) |
\[\left[ {10;15} \right)\] |
\[\left[ {15;20} \right)\] |
\[\left[ {20;25} \right)\] |
\[\left[ {25;30} \right)\] |
\[\left[ {30;35} \right)\] |
|
Số ngày tập của Hưng |
\[2\] |
\[14\] |
\[8\] |
\[3\] |
\[3\] |
|
Số ngày tập của Bình |
\[12\] |
\[8\] |
\[7\] |
\[3\] |
\[0\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.