Trong không gian với hệ trục tọa độ \[Oxyz,\] xét mô hình phòng không như sau: rada đặt tại gốc tọa độ \[O\left( {0\,;0\,;0} \right)\], tên lửa phòng không đặt tại điểm \[M\left( {0\,;50\,;0} \right)\], mỗi đơn vị tương ứng với \[10\,\,{\rm{m}},\] mặt phẳng \[\left( {Oxy} \right)\] trùng với mặt đất, trục \[Oz\] vuông góc mặt đất và hướng lên. Giả sử mọi UAV (phương tiện bay không người lái) và tên lửa đều chuyển động thẳng đều. Tại thời điểm \[t = 0\,\,({\rm{s)}},\] rada phát hiện ra UAV \[A\] ở toạ độ \[{A_0}\left( {1100\,;0\,;15} \right)\]. Tại thời điểm \[t = 1\,\,{\rm{(s)}},\] rađa theo dõi thấy UAV \[A\] ở tọa độ \[{A_1}\left( {1095\,;1\,;14,5} \right)\] trên đường thẳng \[d\]. Tại thời điểm \[t = 6\,\,{\rm{(s)}},\] một tên lửa được phóng lên và chuyển động thẳng đều với vận tốc \[1300\,\,{\rm{(m/s)}},\] va chạm và phá huỷ UAV \[A\] tại điểm \[B\] trên \[d\]. Hỏi sau bao nhiêu giây kể từ lúc được phóng lên thì tên lửa va chạm với UAV (làm tròn kết quả đến hàng phần trăm của giây)?
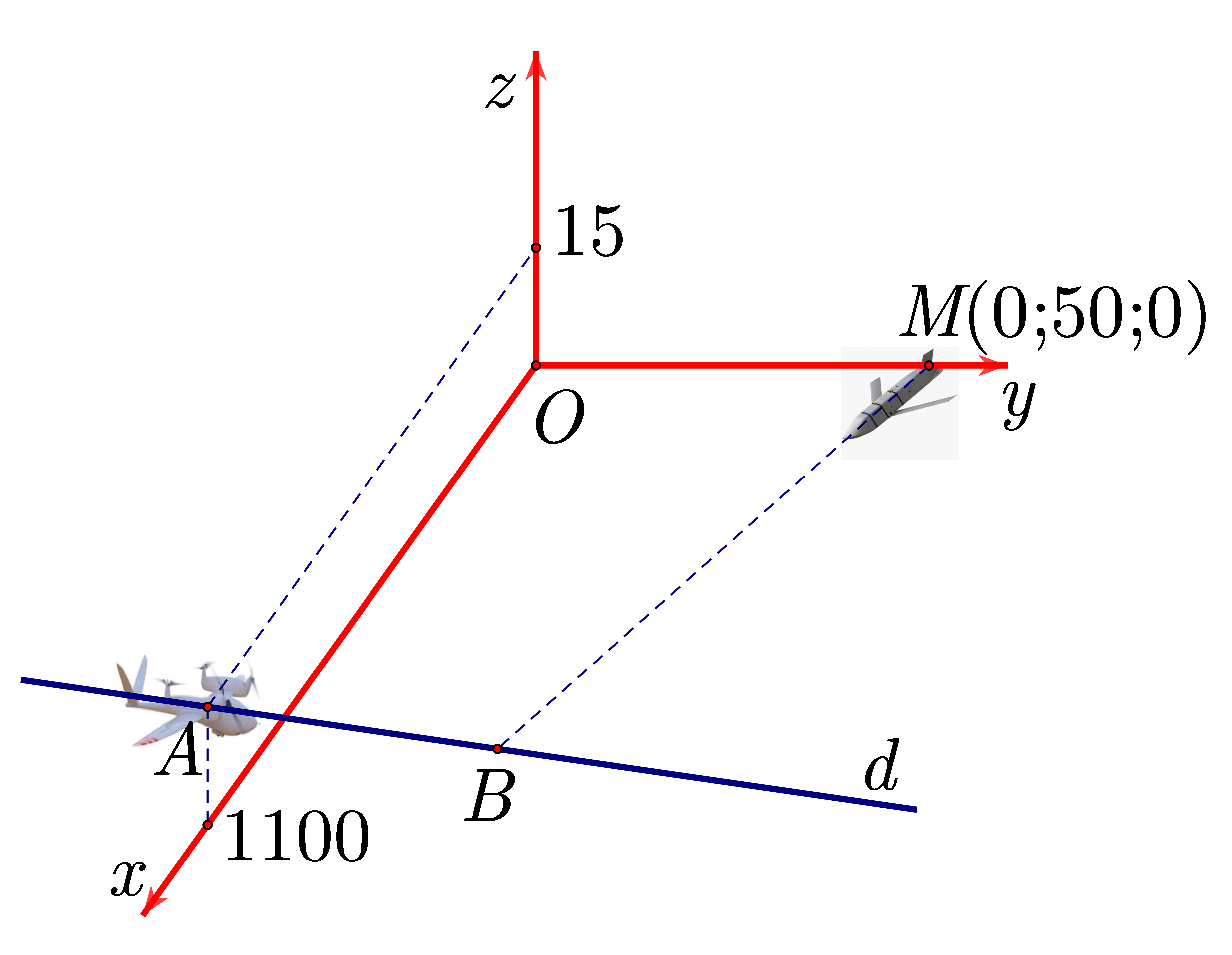
Trong không gian với hệ trục tọa độ \[Oxyz,\] xét mô hình phòng không như sau: rada đặt tại gốc tọa độ \[O\left( {0\,;0\,;0} \right)\], tên lửa phòng không đặt tại điểm \[M\left( {0\,;50\,;0} \right)\], mỗi đơn vị tương ứng với \[10\,\,{\rm{m}},\] mặt phẳng \[\left( {Oxy} \right)\] trùng với mặt đất, trục \[Oz\] vuông góc mặt đất và hướng lên. Giả sử mọi UAV (phương tiện bay không người lái) và tên lửa đều chuyển động thẳng đều. Tại thời điểm \[t = 0\,\,({\rm{s)}},\] rada phát hiện ra UAV \[A\] ở toạ độ \[{A_0}\left( {1100\,;0\,;15} \right)\]. Tại thời điểm \[t = 1\,\,{\rm{(s)}},\] rađa theo dõi thấy UAV \[A\] ở tọa độ \[{A_1}\left( {1095\,;1\,;14,5} \right)\] trên đường thẳng \[d\]. Tại thời điểm \[t = 6\,\,{\rm{(s)}},\] một tên lửa được phóng lên và chuyển động thẳng đều với vận tốc \[1300\,\,{\rm{(m/s)}},\] va chạm và phá huỷ UAV \[A\] tại điểm \[B\] trên \[d\]. Hỏi sau bao nhiêu giây kể từ lúc được phóng lên thì tên lửa va chạm với UAV (làm tròn kết quả đến hàng phần trăm của giây)?

Quảng cáo
Trả lời:
Đáp án: 7,93.
Vectơ vận tốc của UAV: \(\vec v = \overrightarrow {{A_0}{A_1}} = \left( { - 5\,;1\,; - 0,5} \right) \Rightarrow \left| {\vec v} \right| = \frac{{\sqrt {105} }}{2} \Rightarrow v = 5\sqrt {105} {\rm{ (m/s)}}\) (do mỗi đơn vị tương ứng với \[10\,\,{\rm{m}}\]).
Đường bay của UAV là \(d:\left\{ \begin{array}{l}x = 1100 - 5t\\y = t\\z = 15 - 0,5t\end{array} \right.\).
Vị trí của UAV tại thời điểm \(6{\rm{ (s)}}\): \(N\left( {1070\,;6\,;12} \right)\).
Yêu cầu bài toán là tìm điểm \(B \in d\) sao cho \(\frac{{10BN}}{{5\sqrt {105} }} = \frac{{10BM}}{{1300}} \Leftrightarrow 1690000B{N^2} = 2625B{M^2}\)
\[ \Rightarrow 1690000\left[ {{{\left( {30 - 5t} \right)}^2} + {{\left( {t - 6} \right)}^2} + {{\left( {3 - 0,5t} \right)}^2}} \right] = 2625\left[ {{{\left( {1100 - 5t} \right)}^2} + {{\left( {t - 50} \right)}^2} + {{\left( {15 - 0,5t} \right)}^2}} \right]\]
\[ \Leftrightarrow 44293593,75{t^2} - 503173125t - 1586353125 = 0 \Rightarrow t = 13,93083295\].
Vậy từ lúc tên lửa phóng lên cho đến lúc va chạm UAV \[A\] là: \(t \approx 13,93 - 6 = 7,93\,\,{\rm{(s)}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 50.
Ta có giá bán cho mỗi tấn sản phẩm là \(p\left( x \right) = 90 - 0,01{x^2}\) (triệu đồng).
Nên bán \(x\) tấn sản phẩm thu được \(\left( {90 - 0,01{x^2}} \right)x\) (triệu đồng). Điều kiện \(0 < x \le 100\).
Lợi nhuận hàng tháng của nhà máy \(A\) khi sản xuất và bán \(x\) tấn sản phẩm cho nhà máy \(B\) là:
\(L\left( x \right) = \left( {90 - 0,01{x^2}} \right)x \cdot 90\% - \frac{1}{2}\left( {200 + 27x} \right)\) (triệu đồng).
Hay \(L\left( x \right) = - 0,009{x^3} + 67,5x - 100\).
Xét hàm số \(L\left( x \right) = - 0,009{x^3} + 67,5x - 100\) trên nửa khoảng \(\left( {0;100} \right]\):
\(L'\left( x \right) = - 0,027{x^2} + 67,5\);
\(L'\left( x \right) = 0 \Leftrightarrow - 0,027{x^2} + 67,5 = 0 \Leftrightarrow {x^2} = 2500 \Rightarrow x = 50\).
Bảng biến thiên:
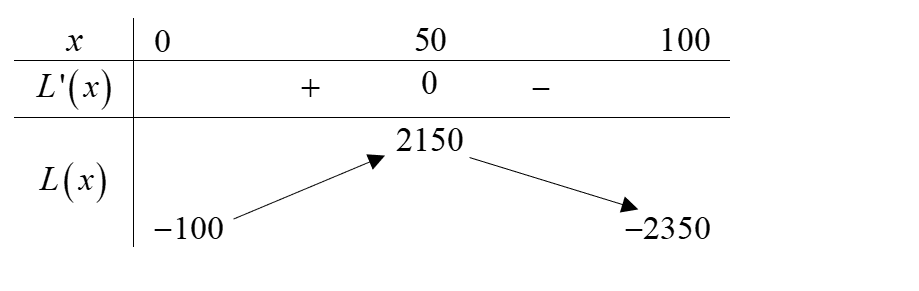
Như vậy nhà máy \(A\) cần sản xuất và bán \(50\) tấn sản phẩm cho nhà máy \(B\) mỗi tháng để thu được lợi nhuận cao nhất.
Lời giải
Đáp án: 711.
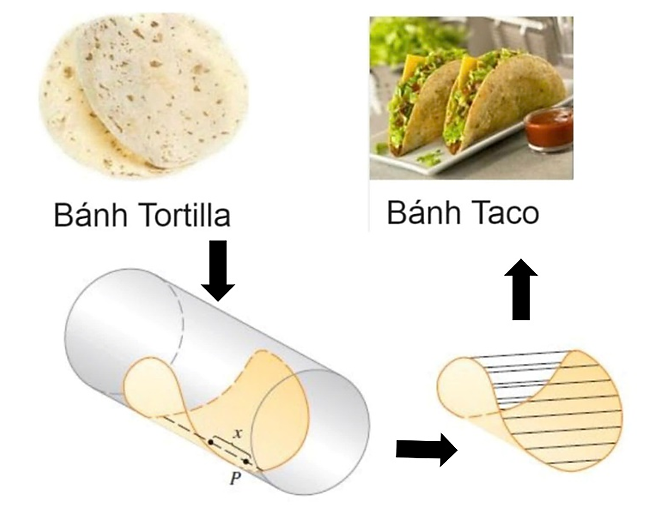
Chu vi của đường tròn có bán kính bằng 4 là \(2 \cdot 4\pi \approx 25,133\).
Như vậy khi trải miếng bánh có đường kính 20 thì còn thừa hai đầu là \(2 \cdot 4\pi - 20 \approx 5,133\).
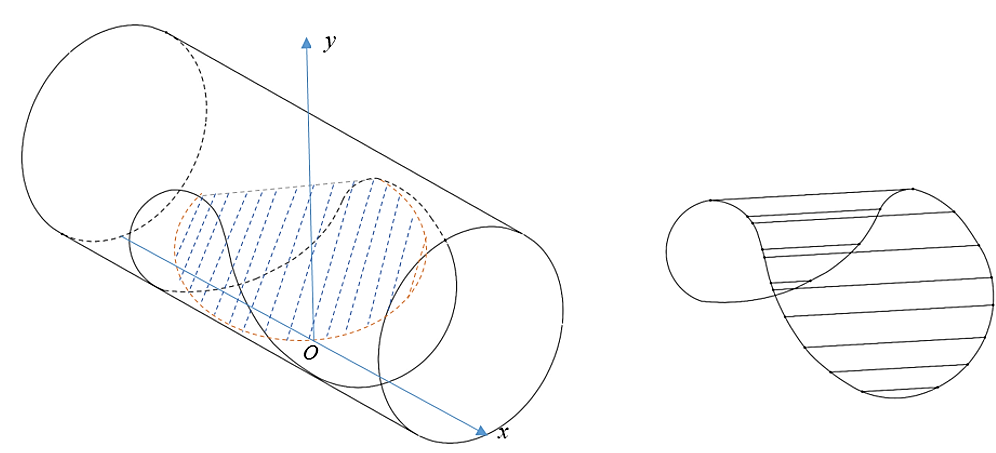
Xét mặt cắt ngang của miếng bánh, mỗi mặt cắt vuông góc với trục tọa độ \(Ox\) là một hình quạt.
Gọi \(x\,,\, - 10 \le x \le 10\) là hoành độ của mặt phẳng cắt trên. Chọn hệ trục tọa độ như hình vẽ.
Ta có .
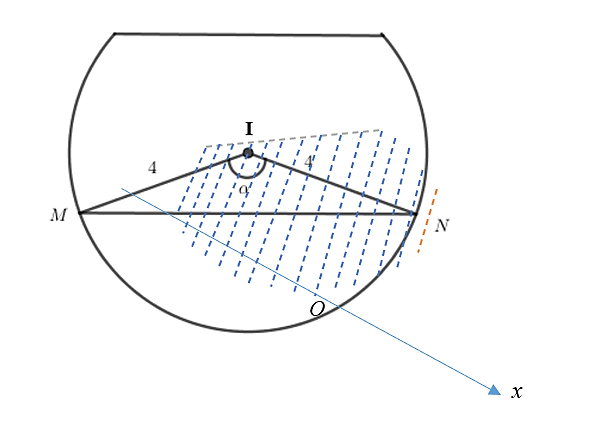
Diện tích mặt cắt
\[S\left( x \right) = \frac{{MN}}{2} \cdot R - {S_{\Delta IMN}} = \frac{{2\sqrt {{{10}^2} - {x^2}} \cdot 4}}{2} - \frac{1}{2}{4^2}\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right) = 4\sqrt {{{10}^2} - {x^2}} - 8\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right)\].
Khi đó thể tích chiếc bánh là:
\[V = 2\int\limits_0^{10} {S\left( x \right){\rm{d}}x = } 2\int\limits_0^{10} {\left[ {4\sqrt {{{10}^2} - {x^2}} - 8\sin \left( {\frac{{\sqrt {{{10}^2} - {x^2}} }}{2}} \right)} \right]{\rm{d}}x \approx 711\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)} \].
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
Thời gian (phút)
\[\left[ {10;15} \right)\]
\[\left[ {15;20} \right)\]
\[\left[ {20;25} \right)\]
\[\left[ {25;30} \right)\]
\[\left[ {30;35} \right)\]
Số ngày tập của Hưng
\[2\]
\[14\]
\[8\]
\[3\]
\[3\]
Số ngày tập của Bình
\[12\]
\[8\]
\[7\]
\[3\]
\[0\]
Khoảng biến thiên của mẫu số liệu ghép nhóm về thời gian tập của Hưng và Bình lần lượt là
Bảng sau thống kê thời gian tập thể dục mỗi ngày trong tháng 3/2025 của hai bạn Hưng và Bình.
|
Thời gian (phút) |
\[\left[ {10;15} \right)\] |
\[\left[ {15;20} \right)\] |
\[\left[ {20;25} \right)\] |
\[\left[ {25;30} \right)\] |
\[\left[ {30;35} \right)\] |
|
Số ngày tập của Hưng |
\[2\] |
\[14\] |
\[8\] |
\[3\] |
\[3\] |
|
Số ngày tập của Bình |
\[12\] |
\[8\] |
\[7\] |
\[3\] |
\[0\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.