Một người điều khiển xe Taxi xuất phát từ trạm thu phí muốn nhập làn vào đường cao tốc, chuyển động tăng tốc với tốc độ (m/s) (trong đó, \[t\] là thời gian tính bằng giây kể từ khi Taxi chuyển động rời trạm thu phí). Từ trạm thu phí đó, một xe Cứu thương cũng xuất phát, chuyển động thẳng cùng hướng với xe Taxi nhưng chậm hơn \[1\] giây so với xe Taxi và có gia tốc bằng \(a\) \[{\rm{(m/}}{{\rm{s}}^{\rm{2}}}{\rm{)}}\](\(a\) là hằng số). Sau khi xe Cứu thương xuất phát được \[17\] giây thì đuổi kịp xe Taxi. Biết rằng, xe Taxi nhập làn cao tốc sau \[20\] giây và cả hai xe duy trì sự tăng tốc trong \[28\] giây kể từ khi Taxi rời trạm thu phí.
a) Quãng đường (kết quả làm tròn đến hàng đơn vị) xe Taxi đi được từ trạm thu phí đến khi nhập làn khoảng \[{\rm{187 m}}\].
Một người điều khiển xe Taxi xuất phát từ trạm thu phí muốn nhập làn vào đường cao tốc, chuyển động tăng tốc với tốc độ (m/s) (trong đó, \[t\] là thời gian tính bằng giây kể từ khi Taxi chuyển động rời trạm thu phí). Từ trạm thu phí đó, một xe Cứu thương cũng xuất phát, chuyển động thẳng cùng hướng với xe Taxi nhưng chậm hơn \[1\] giây so với xe Taxi và có gia tốc bằng \(a\) \[{\rm{(m/}}{{\rm{s}}^{\rm{2}}}{\rm{)}}\](\(a\) là hằng số). Sau khi xe Cứu thương xuất phát được \[17\] giây thì đuổi kịp xe Taxi. Biết rằng, xe Taxi nhập làn cao tốc sau \[20\] giây và cả hai xe duy trì sự tăng tốc trong \[28\] giây kể từ khi Taxi rời trạm thu phí.
a) Quãng đường (kết quả làm tròn đến hàng đơn vị) xe Taxi đi được từ trạm thu phí đến khi nhập làn khoảng \[{\rm{187 m}}\].
Quảng cáo
Trả lời:
Gọi \(t\) là thời gian tính từ lúc xe Taxi bắt đầu chuyển động (\(t \ge 0\), đơn vị giây).
Vận tốc của xe Taxi: \({v_T}\left( t \right) = - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t\) (m/s).
Xe Cứu thương xuất phát sau 1 giây (\(t = 1\)) với gia tốc \(a\) và vận tốc ban đầu \(0\).
Gọi \(t' = t - 1\) là thời gian chuyển động của xe Cứu thương (\(t' \ge 0\)).
Vận tốc xe Cứu thương: \({v_A}\left( {t'} \right) = at'\).
Quãng đường xe Cứu thương: \({S_A}\left( {t'} \right) = \frac{1}{2}a{\left( {t'} \right)^2}\).
a) Sai. Quãng đường xe Taxi đi được đến khi nhập làn (\(t = 20\)\[{\rm{s}}\]):
\({S_T}\left( {20} \right) = \int\limits_0^{20} {{v_T}\left( t \right)\,{\rm{d}}t} = \int\limits_0^{20} {\left( { - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t} \right){\rm{d}}t} \) \[ = \left. {\left( { - \frac{{{t^3}}}{{540}} + \frac{{58}}{{135}}{t^2}} \right)} \right|_0^{20} = - \frac{{{{20}^3}}}{{540}} + \frac{{58}}{{135}} \cdot {20^2} = \frac{{4240}}{{27}} \approx 157\,{\rm{(m)}}\].
Câu hỏi cùng đoạn
Câu 2:
b) Xe Cứu thương chuyển động với gia tốc \(a = \frac{{300}}{{289}}\) \[{\rm{(m/}}{{\rm{s}}^{\rm{2}}}{\rm{)}}\].
b) Xe Cứu thương chuyển động với gia tốc \(a = \frac{{300}}{{289}}\) \[{\rm{(m/}}{{\rm{s}}^{\rm{2}}}{\rm{)}}\].
b) Sai. Xe Cứu thương xuất phát được \[17\] giây thì đuổi kịp Taxi. Tức là tại \(t' = 17{\rm{s}}\) (ứng với \(t = 18{\rm{s}}\) của Taxi).
Tại \(t = 18\), quãng đường hai xe đi được bằng nhau:
\({S_T}\left( {18} \right) = \int\limits_0^{18} {{v_T}\left( t \right)\,{\rm{d}}t} = \int\limits_0^{18} {\left( { - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t} \right){\rm{d}}t} = \left. {\left( { - \frac{{{t^3}}}{{540}} + \frac{{58}}{{135}}{t^2}} \right)} \right|_0^{18} = - \frac{{{{18}^3}}}{{540}} + \frac{{58}}{{135}} \cdot {18^2} = \frac{{642}}{5}\,{\rm{(m)}}\).
\({S_A}\left( {17} \right) = \frac{1}{2}a \cdot {17^2} = \frac{{289}}{2}a\).
\({S_T}\left( {18} \right) = {S_A}\left( {17} \right) \Rightarrow \frac{{642}}{5} = \frac{{289}}{2}a \Rightarrow a = \frac{{1284}}{{1445}}\,\,{\rm{(m/}}{{\rm{s}}^{\rm{2}}}{\rm{)}}\).
Câu 3:
c) Sai. Vận tốc xe Cứu thương khi đuổi kịp Taxi (\(t' = 17{\rm{s}}\)):
\({v_A}\left( {17} \right) = a \cdot t' = \frac{{1284}}{{1445}} \cdot 17 = \frac{{1284}}{{5 \times {{17}^2}}} \cdot 17 = \frac{{1284}}{{85}} \approx 15\,\,({\rm{m/s}})\).
Câu 4:
d) Đúng. Vận tốc trung bình từ lúc gặp nhau (\(t = 18\)) đến \(t = 28\):
Vận tốc trung bình của xe Taxi từ lúc \[t = 18{\rm{s}}\] đến \[t = 28{\rm{s}}\]:
\[{v_T}\left( {TB} \right) = \frac{{\int\limits_{18}^{28} {v\left( t \right)\,{\rm{d}}t} }}{{28 - 18}} = \frac{{\int\limits_{18}^{28} {\left[ { - \frac{1}{{180}}{t^2} + \frac{{116}}{{135}}t} \right]\,{\rm{d}}t} }}{{28 - 18}} = \frac{{\frac{{1510}}{9}}}{{10}} = \frac{{151}}{9} \approx 16,78\,\,({\rm{m/s}})\].
Vận tốc trung bình của xe Cứu thương từ lúc \[t = 17{\rm{s}}\] đến \[t = 27{\rm{s}}\]
\({S_A}\left( {27} \right) = \frac{1}{2}a{.27^2} = \frac{1}{2} \cdot \frac{{1284}}{{1445}} \cdot 729 = \frac{{468018}}{{1445}}\,\,({\rm{m}})\).
\({S_A}\left( {17} \right) = \frac{1}{2} \cdot \frac{{1284}}{{1445}} \cdot {17^2} = \frac{{642}}{5}\) (m).
\[{v_A}\left( {TB} \right) = \frac{{{S_A}\left( {27} \right) - {S_A}\left( {17} \right)}}{{27 - 17}} = \frac{{\frac{{468018}}{{1445}} - \frac{{642}}{5}}}{{10}} \approx 19,55\,\,\left( {{\rm{m/s}}} \right)\].
Do đó \[{v_A}\left( {TB} \right) > {v_T}\left( {TB} \right)\] hay trong khoảng thời gian kể từ lúc hai xe gặp nhau cho đến giây thứ \[28\] (kể từ khi Taxi chuyển động rời trạm thu phí) vận tốc trung bình của xe Cứu thương lớn hơn vận tốc trung bình của xe Taxi.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 3390.
Chọn hệ trục tọa độ \(Oxy\) sao cho parabol \(f\left( x \right) = a{x^2} + bx + c\) cắt trục hoành tại các điểm \(\left( { - 4;0} \right)\), \(\left( {24;0} \right)\) và tọa độ đỉnh \(I\left( {10; - \frac{{17}}{2}} \right)\).
Ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}\begin{array}{l}16a - 4b + c = 0\\576a + 24b + c = 0\,\,\,\,\,\,\end{array}\\{100a + 10b + c = - \frac{{17}}{2}}\end{array}} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{17}}{{392}}\\b = - \frac{{85}}{{98}}\\c = - \frac{{204}}{{49}}\end{array} \right.\).
Nên \(f\left( x \right) = \frac{{17}}{{392}}{x^2} - \frac{{85}}{{98}}x - \frac{{204}}{{49}}\).
Thể tích của quả bóng bầu dục là:
\(V = \pi \int\limits_{ - 4}^{24} {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x = \pi } \int\limits_{ - 4}^{24} {{{\left[ {\frac{{17}}{{392}}{x^2} - \frac{{85}}{{98}}x - \frac{{204}}{{49}}} \right]}^2}{\rm{d}}x = } \frac{{16184\pi }}{{15}}\)\( \approx 3390\) (\({\rm{c}}{{\rm{m}}^{\rm{3}}}\)).
Lời giải
Đáp án: 3,74.
Giả sử chi phí sản xuất các mặt hình trụ là như nhau và các mép nối không đáng kể.
Ta có, thể tích hình trụ là \(V = \pi {r^2}h = 330{\rm{ (ml)}} = 330{\rm{ (c}}{{\rm{m}}^3}) \Rightarrow h = \frac{{330}}{{\pi {r^2}}}{\rm{ (cm)}}\).
Diện tích toàn phần của hộp đựng là: \(S\left( r \right) = 2\pi {r^2} + 2\pi r \cdot h = 2\pi {r^2} + \frac{{660}}{r}\).
Ta có \(S'\left( r \right) = 4\pi r - \frac{{660}}{{{r^2}}}\); \(S'\left( r \right) = 0 \Rightarrow {r^3} = \frac{{165}}{\pi } \Rightarrow r = \sqrt[3]{{\frac{{165}}{\pi }}} \approx {\rm{3,74 (cm)}}\).
Bảng biến thiên:
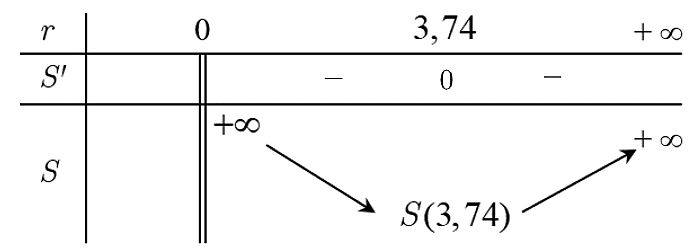
Vậy \(r = \sqrt[3]{{\frac{{165}}{\pi }}} \approx 3,74{\rm{ (cm)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
