Cho lục giác ABCDEF có các đỉnh thuộc đường tròn (O). Biết AB ∕∕DE, BC ∕∕ EF. Khi đó:
A. \[\widehat {ADC} = \widehat {DFA}.\]
B. \[\widehat {ABC} = \widehat {DAF}\].
C. \[\widehat {ADC} = \widehat {DAF}\].
D. \[\widehat {ACD} = \widehat {DAF}\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
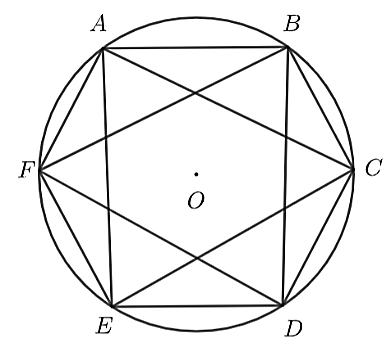
Do BC ∕∕ EF suy ra
\[\widehat {EDC} = \widehat {FAB}\], suy ra \[\widehat {EAC} = \widehat {BDF}\](Do BC ∕∕ EF thì hay FB = EC)
Do AB ∕∕ ED suy ra \[\widehat {AFE} = \widehat {BCD}\], suy ra \[\widehat {BFD} = \widehat {ACE}\]
(Do AB ∕∕ ED thì hay AE = BD)
Từ đây, ta xét ∆AEC và ∆BFD, có: \[\left\{ \begin{array}{l}\widehat {AEC} = 180^\circ - \widehat {EAC} - \widehat {ACE}\\FBD = 180^\circ - \widehat {BFD} - \widehat {BDF}\end{array} \right.\].
Suy ra \[\widehat {FBD} = \widehat {AEC}\], do đó .
Suy ra \[\widehat {ADC} = \widehat {DAF}\] (góc nội tiếp chắn hai cung bằng nhau).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \[\widehat {DMB} = \widehat {ADC}\].
B. \[\widehat {DBM} = \widehat {ADC}\].
C. \[\widehat {DMB} = \widehat {ACD}\].
D. \[\widehat {DMB} = \widehat {ABD}\].
Lời giải
Đáp án đúng là: A
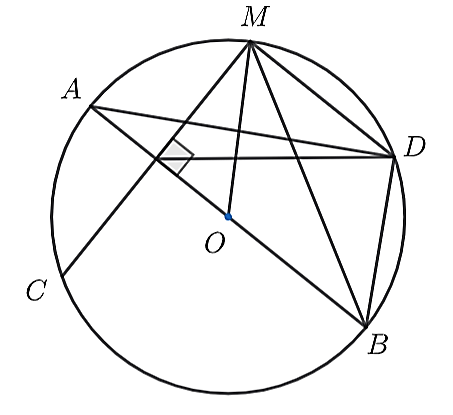
Ta có:
\[\widehat {DMB} = \widehat {DAC}\] (cùng chắn cung DB)Có AB ⊥ MC suy ra (đường kính vuông góc với một dây)
Ta lại có MD ∕∕ AB suy ra (hai cung chắn giữa hai dây song song)
Do đó nên \[\widehat {DMB} = \widehat {ADC}\] (góc nội tiếp chắn hai cung bằng nhau)
Câu 2
A. \[\widehat {ACI} = \widehat {IBD}.\]
B. \[\widehat {CAI} = \widehat {IBD}.\]
C. \[\widehat {ACI} = \widehat {IDB}.\]
D. \[\widehat {ACI} = \widehat {IAC}.\]
Lời giải
Đáp án đúng là: A
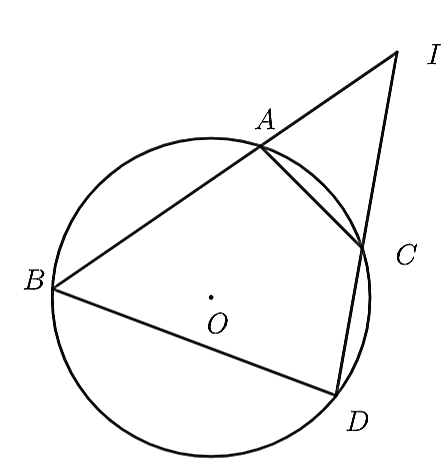
Vì ABCD là tứ giác nội tiếp (O) nên
\[\widehat {ACD} + \widehat {ABD} = 180^\circ \]
Mà \[\widehat {ACD} + \widehat {ACI} = 180^\circ \] (hai góc kề bù)
Do đó, \[\widehat {ACI} = \widehat {ABD}\] hay \[\widehat {ACI} = \widehat {IBD}.\]
Câu 3
A. \[\widehat {ADB} = \widehat {CDM}\].
B. \[\widehat {ABD} = \widehat {CMD}\].
C. \[\widehat {ADB} = \widehat {DCM}\].
D. \[\widehat {ABD} = \widehat {CDM}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho nửa đường tròn (O) đường kính AB và dây AC. Lấy N là điểm chính giữa cung CB. Ta có góc CAN bằng
A. Góc NAB.
B. Góc NBA.
C. Góc ANB.
D. Góc ANC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\widehat {BID} = \widehat {AJE}.\]
B. \[\widehat {BID} = 2\widehat {AJE}.\]
C. \[2\widehat {BID} = \widehat {AJE}.\]
D. Tất cả các đáp án đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[\widehat {MCA}.\]
B. \[\widehat {ABH}\].
C. \[\widehat {MCO}\].
D. \[\widehat {AMC}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo