Cho hai đường tròn (O) và (O') cắt nhau ở A và B, O nằm trên đường tròn (O'). Dây AC của (O) cắt (O') ở D, dây OE của (O') cắt (O) ở F như hình bên. Chọn khẳng định sai.
A. \[\widehat {BOD} = \widehat {BOC}\].
B. \[\widehat {BOD} = \widehat {DOC}\].
C. OD là đường trung tuyến trong ∆BOC.
D. OD ⊥ BC.
Quảng cáo
Trả lời:
Đáp án đúng là: A
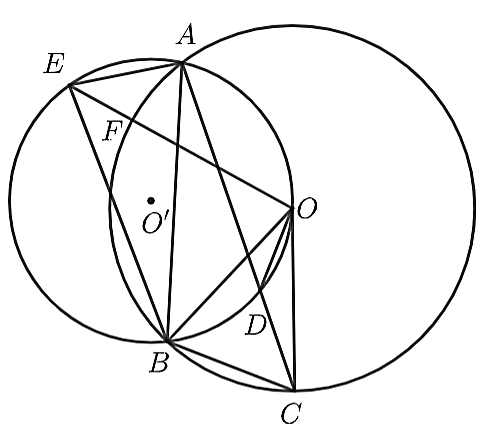
Dựng hai bán kính OB, OC của (O).
Xét đường tròn (O') ta có .
Mà suy ra (1)
Xét đường tròn (O) ta có: (2).
Từ (1) và (2) ta được \[\widehat {BOD} = \frac{1}{2}\widehat {BOC}\] suy ra \[\widehat {BOD} = \widehat {DOC}\] hay OD là tia phân giác \[\widehat {BOC}\].
Ta lại có ∆BOC cân tại O nên OD vừa là phân giác vừa là đường cao, đường trung tuyến trong tam giác BOC.
Do đó, OD ⊥ BC.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Chỉ (I) đúng.
B. Chỉ (I), (II) đúng.
C. Chỉ (II), (III) đúng.
D. Cả (I), (II), (III) đúng.
Lời giải
Đáp án đúng là: D
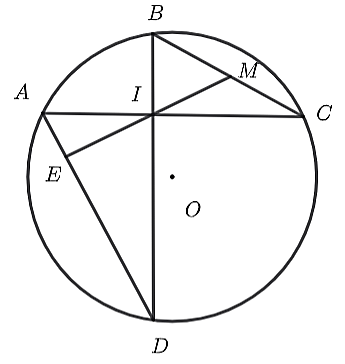
Gọi E là giao điểm của IM và AD.
Ta có: AC ⊥ BD tại I nên ∆BCI vuông tại I.
Mà MB = MC nên MI = MB (tính chất đường trung tuyến trong tam giác vuông).
Do đó, ∆MBI cân.
Suy ra \[\widehat {MIB} = \widehat {MBI}\] mà \[\widehat {NID} = \widehat {BIM}\] đối đỉnh do đó \[\widehat {MBI} = \widehat {NID}\].
Ta có: \[\widehat {BDA} = \widehat {BCA}\](góc nội tiếp chắn cung AB)
Mà \[\widehat {BCA} + \widehat {MBI} = 90^\circ \] (tam giác BIC vuông tại I).
Suy ra \[\widehat {NID} + \widehat {BDA} = 90^\circ \] hay \[\widehat {AEI} = 90^\circ \] hay MI ⊥ AD.
Câu 2
A. (I) và (III).
B. (II) và (III).
C. (I) và (II).
D. (I), (II) và (III).
Lời giải
Đáp án đúng là: C
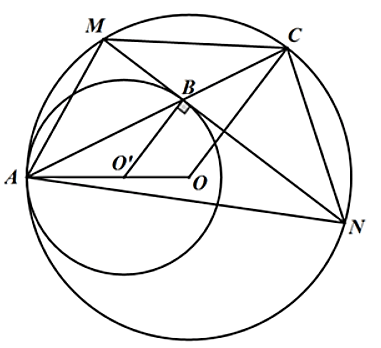
Vì ∆O
'AB cân tại O' nên \[\widehat {O'AB} = \widehat {O'BA}\].∆OAC cân tại O nên \[\widehat {OAC} = \widehat {OCA}\].
Suy ra \[\widehat {OCA} = \widehat {O'BA}\], mà hai góc này ở vị trí đồng vị, do đó, O'B // OC.
Mặt khác MN là tiếp tuyến của (O') tại B.
Do đó, O'B ⊥MN. Suy ra OC ⊥ MN.
Trong đường tròn (O), có ON là đường trung trực của MN.
Suy ra CM = CN từ đó .
Do đó, \[\widehat {MAC} = \widehat {NAC}\].
Hay AC là phân giác của góc MAN.
Câu 3
A. MN // BC.
B. BM > CN.
C. BM = CN.
D. \[\widehat {ANM} = 90^\circ \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. Cả (I), (II) đều đúng.
D. Cả (I), (II) đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. AH ⊥ BC.
B. OM // AH.
C. \[HM = \frac{{HF}}{2}.\]
D. OM ⊥ BF.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 3.
B. 2.
C. 1.
D. 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.