Câu hỏi:
27/05/2025 47Cho tam giác ABC cân tại A có \[\widehat {BAC} = 120^\circ \], trên nửa mặt phẳng bờ BC không chứa đỉnh A, lấy D sao cho BCD là tam giác đều. Khi đó
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
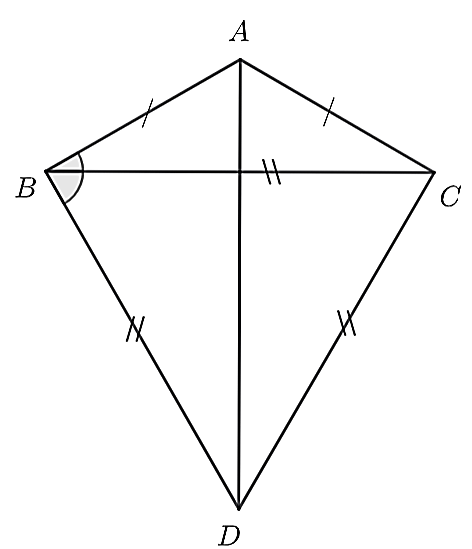
Ta có tam giác BCD là tam giác đều nên
\[\widehat {BCD} = 60^\circ \] (1).
Mặt khác ∆ABC là tam giác cân tại A có \[\widehat {BAC} = 120^\circ \] hơn nữa tổng ba góc trong một tam giác bằng 180° nên ta có:
\[\left\{ \begin{array}{l}\widehat {ACB} = \widehat {ABC}\\\widehat {ABC} + \widehat {ACB} + \widehat {BAC} = 180^\circ \end{array} \right.\], suy ra \[\widehat {BCA} = 30^\circ \] (2)
Từ (1) và (2) suy ra \[\widehat {DCA} = \widehat {DCB} + \widehat {BCD} = 60^\circ + 30^\circ = 90^\circ \].
Tương tự ta chứng minh được \[\widehat {DBA} = 90^\circ \].
Do đó, ∆ACD vuông tại C nên A, C, D thuộc đường tròn đường kính AD. (3)
∆ABD vuông tại B nên A, B, D thuộc đường tròn đường kính AD. (4)
Từ (3) và (4) suy ra bốn điểm A, B, C, D cùng thuộc một đường tròn.
Vậy tứ giác ABDC là tứ giác nội tiếp.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
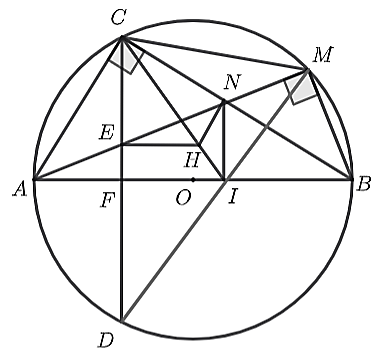
• Ta có: \[\widehat {BMA} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn) hay \[\widehat {BME} = 90^\circ \]
Xét ∆BME vuông tại M nên B, M ,E thuộc đường tròn đường kính BE (1)
Xét ∆EFB vuông tại F nên B, F, E thuộc đường tròn đường kính BE (2)
Từ (1) và (2) suy ra B, M, E, F cùng thuộc đường tròn đường kính BE hay tứ giác BMEF nội tiếp.
Do đó, (I) đúng.
• Ta có AB ⊥ CD tại F và AB là đường kính
Ta chứng minh được ∆OCD cân tại O do OC = OD = R nên F là trung điểm của CD.
Do đó, AB là đường trung trực của CD nên .
Ta có: và .
Suy ra \[\widehat {CMA} = \widehat {DMA}\], do đó AM là phân giác của góc CMD.
Vậy ý (II) đúng.
• Xét ∆ACE và ∆ACM có:
\[\widehat A\] chung (gt)
Suy ra ∆ACE ᔕ ∆ACM (g.g)
Suy ra \[\frac{{AC}}{{AM}} = \frac{{AE}}{{AC}}\] hay AC2 = AE.AM.
Do đó ý (III) đúng.
Vậy cả ba phát biểu trên đều đúng.
Lời giải
Đáp án đúng là: C
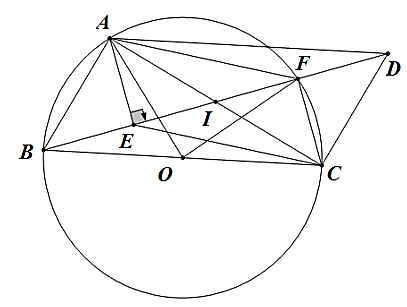
• Ta có: \[\widehat {BAC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn).
Mà ABCD là hình bình hành nên AB // CD.
Do đó, \[\widehat {ACD} = \widehat {BAC} = 90^\circ \] (so le trong)
Suy ra ∆ACD vuông tại C nên A, C, D thuộc đường tròn đường kính AD (1).
∆ADE vuông tại E nên E, A, D thuộc đường tròn đường kính AD (2).
Từ (1) và (2) suy ra A, E, C, D cùng thuộc một đường tròn hay tứ giác AEDC nội tiếp.
Do đó, ý (I) đúng.
• Do tứ giác AEDC nội tiếp nên \[\widehat {CAE} = \widehat {CDE}\] (góc nội tiếp chắn cung EC)
Mà AB // CD nên \[\widehat {CDE} = \widehat {ABD}\] (so le trong)
Suy ra \[\widehat {CAE} = \widehat {ABD}\]. (3)
Mà \[\widehat {ABD}\] là góc nội tiếp chắn cung AF, \[\widehat {AOF}\] là góc ở tâm chắn cung AF nên \[\widehat {AOF} = 2\widehat {ABD}\]. (4)
Từ (3) và (4) suy ra \[\widehat {AOF} = 2\widehat {CAE}\].
Do đó, ý (II) sai.
• Ta có: \[\widehat {BFC} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn) hay FC ⊥ BD.
Có AE ⊥ BD nên FC // AE.
Lại có \[\widehat {AFB} = \widehat {ACB} = \widehat {CAD} = \widehat {FEC}\] nên AF // EC.
Do đó, tứ giác AECF là hình bình hành.
Suy ra, ý (III) đúng.
• Gọi giao điểm của AC và BD là I, do tứ giác ABCD là hình bình hành nên AI = IC; IB = ID; AB = CD.
Xét ∆DIC vuông tại C có CF ⊥ BD
Chứng minh được ∆CDI ᔕ ∆FDC (g.g) suy ra \[\frac{{CD}}{{FD}} = \frac{{DI}}{{DC}}\] hay CD2 = FD.DI.
Mà AB = DC nên AB2 = DF.DI.
Suy ra 2AB2 = 2.DF.DI mà 2DI = BD do đó, 2AB2 = DF.DB.
Do đó, ý (IV) đúng.
Vậy có 3 phát biểu đúng là (I), (III), (IV).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
-
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 1. Phương trình quy về phương trình bậc nhất một ẩn có đáp án
Nhắn tin Zalo