Cho hình chóp \[S.ABC\], đáy ABC có \[AB = 10{\rm{ cm}}\], \[BC = 12{\rm{ cm}}\], \[AC = 14{\rm{ cm}}\], các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau và đều bằng \[\alpha \] thỏa mãn \[\tan \alpha = 3\]. Thể tích khối chóp \[S.ABC\] là
Quảng cáo
Trả lời:
Nửa chu vi tam giác \(ABC\) là:
\[p = \frac{{AB + BC + AC}}{2} = 18\,\,{\rm{(cm)}}\].
Theo công thức Heron, diện tích tam giác \(ABC\) là:
\(S = \sqrt {p\left( {p - AB} \right)\left( {p - AC} \right)\left( {p - BC} \right)} = 24\sqrt 6 \) (cm2).
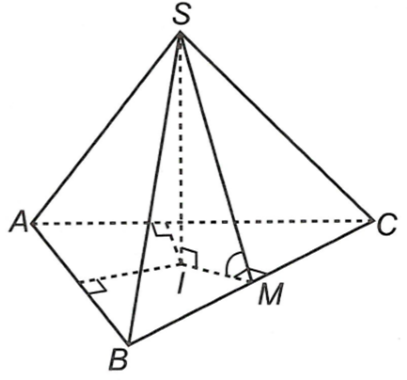
Các mặt bên cùng tạo với mặt phẳng đáy các góc bằng nhau nên hình chiếu của S trên mặt phẳng \[\left( {ABC} \right)\] là tâm \(I\) của đường tròn nội tiếp \[\Delta ABC \Rightarrow SI \bot \left( {ABC} \right)\].
Kẻ \(IM \bot BC\) tại \(M\), từ đó suy ra \(BC \bot SM\).
Do đó, \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {SM,\,IM} \right) = \widehat {SMI} = \alpha \).
Lại có, diện tích tam giác \(ABC\) là: \[S = p \cdot r \Rightarrow IM = r = \frac{S}{p} = \frac{{4\sqrt 6 }}{3}\,\,{\rm{(cm)}}\].
\[\Delta SIM\] vuông tại I có \[SI = IM\tan \alpha = \frac{{4\sqrt 6 }}{3} \cdot 3 = 4\sqrt 6 \,\,{\rm{(cm)}}\].
Vậy \[{V_{S.ABC}} = \frac{1}{3} \cdot S \cdot SI = \frac{1}{3} \cdot 24\sqrt 6 \cdot 4\sqrt 6 = 192\,\,({\rm{c}}{{\rm{m}}^3})\]. Chọn C.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
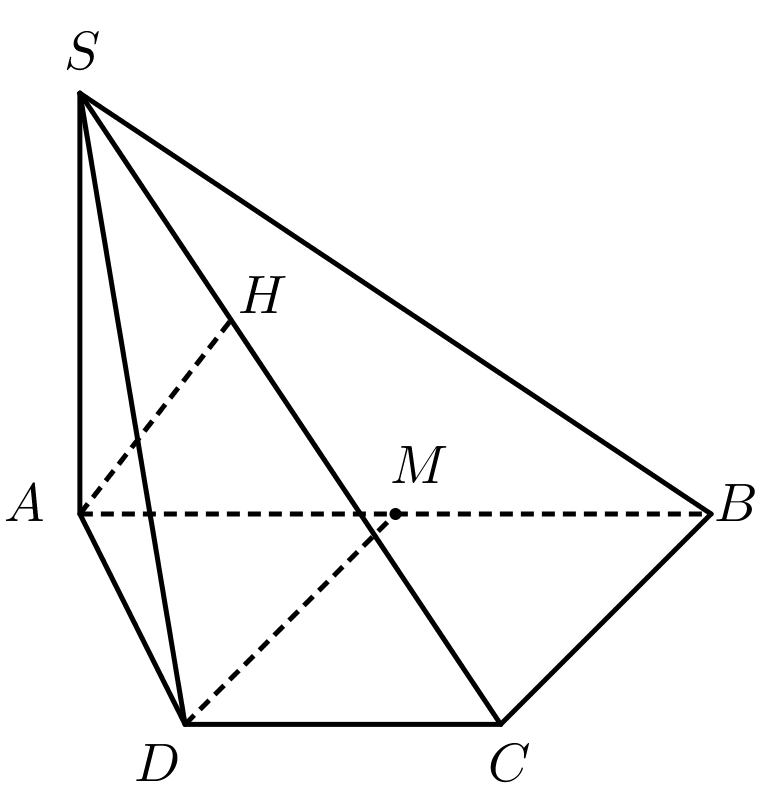
Ta có \[M\] là trung điểm của \[AB\].
Theo giả thiết suy ra \[ABCD\] là nửa lục giác đều nội tiếp đường tròn đường kính \[AB\]\[ \Rightarrow \left\{ \begin{array}{l}\widehat {ACB} = 90^\circ ;\widehat {ABC} = 60^\circ \\AC = \sqrt 3 \end{array} \right.\].
Vì \[DM{\rm{//}}BC \Rightarrow DM{\rm{//}}\left( {SBC} \right)\].
Do đó \[d\left( {DM,SB} \right) = d\left( {DM,\left( {SBC} \right)} \right) = d\left( {M,\left( {SBC} \right)} \right) = \frac{1}{2}d\left( {A,\left( {SBC} \right)} \right)\] (vì \[MB = \frac{1}{2}AB\]).
Kẻ \[AH \bot SC\] tại \[H\]. Ta có \[\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right)\]\[ \Rightarrow AH \bot BC\].
Khi đó \[\left\{ \begin{array}{l}AH \bot SC\\AH \bot BC\end{array} \right. \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH\].
Xét tam giác \[SAC\] vuông tại \[A\], ta có \[A{H^2} = \frac{{A{C^2} \cdot S{A^2}}}{{A{C^2} + S{A^2}}} = \frac{{{{\left( {\sqrt 3 } \right)}^2} \cdot {3^2}}}{{{{\left( {\sqrt 3 } \right)}^2} + {3^2}}} = \frac{9}{4}\]\[ \Rightarrow AH = \frac{3}{2}\].
Vậy \[d\left( {DM,SB} \right) = \frac{1}{2}d\left( {A,\left( {SBC} \right)} \right) = \frac{1}{2}AH = \frac{3}{4} = 0,75\].
Lời giải
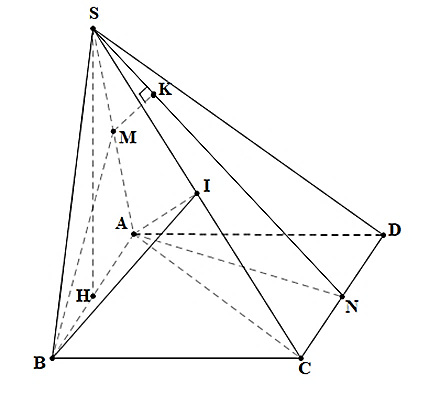
Vì tam giác \(SAB\) đều nên \(SH \bot AB\).
Mà \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).
Tam giác \(SAB\) đều cạnh \(a \Rightarrow SH = \frac{{a\sqrt 3 }}{2}\).
Diện tích hình thoi \(ABCD\):
\({S_{ABCD}} = 2{S_{\Delta ABC}} = 2 \cdot \frac{1}{2}AB \cdot BC \cdot \sin B = \frac{{{a^2}\sqrt 3 }}{2}\).
Vậy thể tích khối chóp \(S.ABCD\): \({V_{S.ABCD}} = \frac{1}{3}SH \cdot {S_{ABCD}} = \frac{1}{3} \cdot \frac{{a\sqrt 3 }}{2} \cdot \frac{{{a^2}\sqrt 3 }}{2} = \frac{{{a^3}}}{4}\).
Dễ thấy \(\Delta ABC\) đều \( \Rightarrow AC = BC = a \Rightarrow \)các tam giác \(SAC\) và \(SBC\) lần lượt cân tại \(A\) và \(B\).
Gọi \(I\) là trung điểm của \(SC \Rightarrow \left\{ \begin{array}{l}SC \bot AI\\SC \bot BI.\end{array} \right.\)
Suy ra \(\widehat {AIB}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,SC,B} \right]\).
Ta có \(S{C^2} = S{H^2} + C{H^2} = \frac{{3{a^2}}}{2} \Rightarrow S{I^2} = I{C^2} = \frac{{3{a^2}}}{8}\).
Suy ra \(I{A^2} = S{A^2} - S{I^2} = \frac{{5{a^2}}}{8}\). Tương tự \(I{B^2} = \frac{{5{a^2}}}{8}\).
Do đó \(\cos \alpha = \cos \widehat {AIB} = \frac{{I{A^2} + I{B^2} - A{B^2}}}{{2 \cdot IA \cdot IB}} = \frac{1}{5}\).
Ta có \(\Delta ACD\)đều \( \Rightarrow AN \bot CD \Rightarrow AN \bot AB \Rightarrow AN \bot \left( {SAB} \right) \Rightarrow \left( {SAN} \right) \bot \left( {SAB} \right)\).
\(\Delta SAB\) đều \( \Rightarrow BM \bot SA \Rightarrow BM \bot \left( {SAN} \right)\).
Dựng \(MK \bot SN\) tại \(K \Rightarrow MK\) là đoạn vuông góc chung của \(BM\) và \(SN\).
Suy ra \(MK = d\left( {BM,SN} \right)\).
Ta có \(MK = MS \cdot \sin \widehat {MSK} = MS \cdot \frac{{AN}}{{SN}} = MS \cdot \frac{{AN}}{{\sqrt {S{A^2} + A{N^2}} }} = \frac{a}{2} \cdot \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt {{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} }} = \frac{{a\sqrt {21} }}{{14}}\).
Vậy \(d\left( {BM,SN} \right) = \frac{{a\sqrt {21} }}{{14}}\).
Đáp án: a) Đúng, b) Sai, c) Sai, d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.