Trong không gian với hệ trục tọa độ \(Oxyz\), có 3 diễn viên xiếc nhào lộn đang ở 3 vị trí \(A\left( {1\,; - 2\,;\,3} \right)\), \(B\left( {3\,;\,4\,;\,1} \right)\), \(C\left( { - 5\,;\,2\,;\,1} \right)\). Gọi \(\left( \alpha \right)\) là một mặt phẳng lưới bảo hộ di động luôn chứa trục hoành sao cho \(A\), \(B\), \(C\) nằm cùng phía với \(\left( \alpha \right)\) và \({d_1},\,{d_2},\,{d_3}\) lần lượt là khoảng cách từ \(A,\) \(B\), \(C\) đến \(\left( \alpha \right)\). Tiết mục xiếc sẽ được bắt đầu khi mặt phẳng \(\left( \alpha \right)\) được điều chỉnh để biểu thức \(T = {d_1} + 2{d_2} + 3{d_3}\) đạt giá trị lớn nhất. Biết \(T\) lớn nhất bằng \(a\sqrt b \) (với \(a \in \mathbb{N}\), \(b\) là số nguyên tố). Hãy tính giá trị của biểu thức \(S = 2{\rm{a}} + 3b\).
Trong không gian với hệ trục tọa độ \(Oxyz\), có 3 diễn viên xiếc nhào lộn đang ở 3 vị trí \(A\left( {1\,; - 2\,;\,3} \right)\), \(B\left( {3\,;\,4\,;\,1} \right)\), \(C\left( { - 5\,;\,2\,;\,1} \right)\). Gọi \(\left( \alpha \right)\) là một mặt phẳng lưới bảo hộ di động luôn chứa trục hoành sao cho \(A\), \(B\), \(C\) nằm cùng phía với \(\left( \alpha \right)\) và \({d_1},\,{d_2},\,{d_3}\) lần lượt là khoảng cách từ \(A,\) \(B\), \(C\) đến \(\left( \alpha \right)\). Tiết mục xiếc sẽ được bắt đầu khi mặt phẳng \(\left( \alpha \right)\) được điều chỉnh để biểu thức \(T = {d_1} + 2{d_2} + 3{d_3}\) đạt giá trị lớn nhất. Biết \(T\) lớn nhất bằng \(a\sqrt b \) (với \(a \in \mathbb{N}\), \(b\) là số nguyên tố). Hãy tính giá trị của biểu thức \(S = 2{\rm{a}} + 3b\).
Quảng cáo
Trả lời:
Cách 1.
Bài toán phụ: Cho mặt phẳng \(\left( P \right)\) với ba điểm \(A\), \(B\), \(C\) nằm cùng phía so với mặt phẳng \(\left( P \right)\). Gọi \(G\) là trọng tâm tam giác \(ABC\); \(A',B',C',G'\) lần lượt là hình chiếu của \(A,B,C,G\) lên mặt phẳng \(\left( P \right)\), khi đó ta có \[AA' + BB' + CC' = 3GG'\].
Trong hệ trục \[Oxyz\] lấy điểm \(A'\) sao cho \(\overrightarrow {OA'} = \frac{1}{6}\overrightarrow {OA} \Rightarrow A'\left( {\frac{1}{6}; - \frac{1}{3};\frac{1}{2}} \right)\) và \({d_1} = 6d\left( {A',\left( \alpha \right)} \right) = 6{d'_1};\)
lấy điểm \(B'\) sao cho \(\overrightarrow {OB'} = \frac{1}{3}\overrightarrow {OB} \Rightarrow B'\left( {1;\frac{4}{3};\frac{1}{3}} \right)\) và \[{d_2} = 3d\left( {B',\left( \alpha \right)} \right) = 3{d'_2}\];
lấy điểm \(C'\) sao cho \(\overrightarrow {OC'} = \frac{1}{2}\overrightarrow {OC} \Rightarrow C'\left( { - \frac{5}{2};1;\frac{1}{2}} \right)\) và \({d_3} = 2d\left( {C',\left( \alpha \right)} \right) = 2{d'_3}\).
Khi đó \[T = {d_1} + 2{d_2} + 3{d_3} = 6\left( {{{d'}_1} + {{d'}_2} + {{d'}_3}} \right) = 6 \cdot 3GG' = 18GG'\] với \(G\left( {\frac{{ - 4}}{9};\frac{2}{3};\frac{4}{9}} \right)\) là trọng tâm tam giác \(A'B'C'\) và \(G'\) là hình chiếu của G lên mặt phẳng \(\left( \alpha \right)\).
Ta lại có \(GG'\, = d\left( {G,\left( \alpha \right)} \right) \le d\left( {G,Ox} \right) = \sqrt {\frac{4}{9} + \frac{{16}}{{81}}} = \frac{{2\sqrt {13} }}{9}\); suy ra \(T \le 4\sqrt {13} \).
Vậy \(S = 2a + 3b = 2 \cdot 4 + 3 \cdot 13 = 47\).
Cách 2.
Ta có \(T = {d_1} + 2{d_2} + 3{d_3} = \left( {{d_1} + {d_2}} \right) + \left( {{d_2} + {d_3}} \right) + 2{d_3}\).
Gọi \(M\), \(N\) lần lượt là trung điểm của \(BA\), \(BC\), ta có \(M\left( {2;1;2} \right)\), \(N\left( { - 1;3;1} \right)\).
Suy ra \({d_1} + {d_2} = 2d\left( {M,\left( \alpha \right)} \right) = 2{d_M}\), \({d_2} + {d_3} = 2d\left( {N,\left( \alpha \right)} \right) = {d_N}\)\( \Rightarrow T = 2{d_M} + 2{d_N} + 2{d_3}\) \(\left( 1 \right)\).
Gọi \(M'\), \(N'\), \(C'\) lần lượt là hình chiếu vuông góc của \(M\), \(N\), \(C\) trên mặt phẳng \(\left( \alpha \right)\).
Gọi \(G\) là trọng tâm tam giác \(MNC\) và \(G'\) là hình chiếu vuông góc của điểm \(G\) trên mặt phẳng \(\left( \alpha \right)\)\( \Rightarrow G\left( { - \frac{4}{3};2;\frac{4}{3}} \right)\).
Theo tính chất của phép chiếu vuông góc, ta suy ra \(G'\) là trọng tâm của tam giác \(M'N'C'\).
Do đó, \(\overrightarrow {G'M'} + \overrightarrow {G'N'} + \overrightarrow {G'C'} = \overrightarrow 0 \).
Mặt khác \(\overrightarrow {MM'} + \overrightarrow {NN'} + \overrightarrow {CC'} = 3\overrightarrow {GG'} \) \(\left( * \right)\).
Và do các vectơ \(\overrightarrow {MM'} \), \(\overrightarrow {NN'} \), \(\overrightarrow {CC'} \), \(\overrightarrow {GG'} \) cùng hướng nên \(\left( * \right)\)\( \Leftrightarrow MM' + NN' + CC' = 3GG'\)
hay \({d_M} + {d_N} + {d_C} = 3{d_G}\)\(\left( 2 \right)\).
Từ \(\left( 1 \right),\left( 2 \right)\) suy ra \(T = 6d\left( {G,\left( \alpha \right)} \right) \le 6d\left( {G,Ox} \right)\).
Gọi \(G''\) là hình chiếu của \(G\) xuống trục \(Ox\)\( \Rightarrow G''\left( { - \frac{4}{3};0;0} \right)\).
Suy ra \(T = 6d\left( {G,\left( \alpha \right)} \right) \le 6d\left( {G,Ox} \right) = 6GG' = 6\sqrt {{2^2} + {{\left( {\frac{4}{3}} \right)}^2}} = 4\sqrt {13} \).
Vậy \(\mathop {\max T}\limits_{} = 4\sqrt {13} \) khi và chỉ khi \(GG' \bot Ox\).
Vậy \(a = 4,b = 13 \Rightarrow 2a + 3b = 47\).
Đáp án: \(47\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
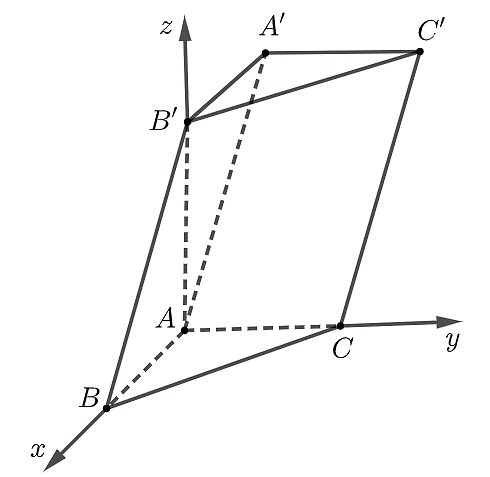
a) Tính được \[\overrightarrow {AB} = \left( {2;0;0} \right),\overrightarrow {AC} = \left( {0;3;0} \right),\overrightarrow {AB'} = \left( {0;0;4} \right) \Rightarrow AB = 2;AC = 3;AB' = 4\].
Có \[Oz \bot \left( {Oxy} \right)\] và \[AB' \subset Oz\], \[\left( {ABC} \right) \equiv \left( {Oxy} \right)\] nên \[AB' \bot \left( {ABC} \right)\].
Thể tích khối lăng trụ \[ABC.A'B'C'\] là:
\[V = d\left( {B',\left( {ABC} \right)} \right) \cdot {S_{\Delta ABC}} = AB' \cdot \frac{1}{2} \cdot AB \cdot AC = 4 \cdot \frac{1}{2} \cdot 2 \cdot 3 = 12\].
b) Gọi \[A'\left( {x;y;z} \right) \Rightarrow \overrightarrow {AA'} = \left( {x;y;z} \right)\].
Có \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], mà \[\overrightarrow {BB'} = \overrightarrow {AA'} \], suy ra toạ độ điểm \[A'\] là \[\left( { - 2;0;4} \right)\].
Từ đó ta có \[\overrightarrow {A'B} = \left( {4;0; - 4} \right),\overrightarrow {A'C} = \left( {2;3; - 4} \right)\]. Vậy \[\overrightarrow u = \overrightarrow {A'B} + \overrightarrow {A'C} \] thì \[\overrightarrow u = \left( {6;3; - 8} \right)\].
c) Gọi \[C'\left( {a;b;c} \right) \Rightarrow \overrightarrow {CC'} = \left( {a;b - 3;c} \right)\].
Ta có \[\overrightarrow {BB'} = \overrightarrow {CC'} \], mà \[\overrightarrow {BB'} = \left( { - 2;0;4} \right)\], suy ra toạ độ điểm \[C'\] là \[\left( { - 2;3;4} \right)\].
d) Hình chiếu vuông góc của điểm \[B\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[A\] (do \[Ox \bot \left( {Oyz} \right)\]).
Do \[Ox\,{\rm{//}}\,A'B'\] mà \[Ox \bot \left( {Oyz} \right)\] nên \[A'B' \bot \left( {Oyz} \right)\], từ đó suy ra hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( {Oyz} \right)\] là điểm \[B'\].
Gọi \[{C_1}\left( {m;n;p} \right)\] là hình chiếu vuông góc của \[C'\] lên mặt phẳng \[\left( {Oyz} \right)\]\[ \Rightarrow {C_1}\left( {0;3;4} \right)\].
Vậy hình chiếu của hình lăng trụ \[ABC.A'B'C'\] lên mặt phẳng \[\left( {Oyz} \right)\]là hình chữ nhật \[AB'{C_1}C\].
Diện tích đa giác là: \[{S_{AB'{C_1}C}} = AB' \cdot AC = 4 \cdot 3 = 12\].
Đáp án: a) Sai, b) Đúng, c) Đúng, d) Sai.
Câu 2
Lời giải
Ta có \[\vec u = 2\vec a - 3\vec b + \vec c = \left( {5\,;\,3\,;\, - 9} \right)\]. Chọn C.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.