2.1. Tính giá trị của biểu thức \[A = 2x + 3{y^2} - 12\] với \[x = - 4\] và \[y = 2.\]
2.2. Cho hai đa thức \[A\left( x \right) = {x^3} - 3{x^2} - x - 4 + 4{x^2} - x\];
\[B\left( x \right) = {x^4} + 2{x^2} - 5x - {x^2} + 6 + {x^3} - {x^4}\].
a) Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của hai đa thức trên.
b) Xác định bậc và hệ số cao nhất của đa thức \(A\left( x \right)\).
c) Tìm nghiệm của đa thức \(M\left( x \right)\) biết \(M\left( x \right) = A\left( x \right) - B\left( x \right)\).
2.1. Tính giá trị của biểu thức \[A = 2x + 3{y^2} - 12\] với \[x = - 4\] và \[y = 2.\]
2.2. Cho hai đa thức \[A\left( x \right) = {x^3} - 3{x^2} - x - 4 + 4{x^2} - x\];
\[B\left( x \right) = {x^4} + 2{x^2} - 5x - {x^2} + 6 + {x^3} - {x^4}\].
a) Thu gọn và sắp xếp đa thức theo lũy thừa giảm dần của hai đa thức trên.
b) Xác định bậc và hệ số cao nhất của đa thức \(A\left( x \right)\).
c) Tìm nghiệm của đa thức \(M\left( x \right)\) biết \(M\left( x \right) = A\left( x \right) - B\left( x \right)\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
2.1. Thay \[x = - 4\] và \[y = 2\] vào biểu thức \[A = 2x + 3{y^2} - 12\], ta được:
\[A = 2.\left( { - 4} \right) + {3.2^2} - 12 = - 8\].
Vậy \[A = - 8\].
2.2. a) \[A\left( x \right) = {x^3} - 3{x^2} - x - 4 + 4{x^2} - x\]
\( = {x^3} + \left( { - 3{x^2} + 4{x^2}} \right) + \left( { - x - x} \right) - 4\)
\( = {x^3} + {x^2} - 2x - 4\).
\[B\left( x \right) = {x^4} + 2{x^2} - 5x - {x^2} + 6 + {x^3} - {x^4}\]
\( = \left( {{x^4} - {x^4}} \right) + {x^3} + \left( {2{x^2} - {x^2}} \right) - 5x + 6\)
\( = {x^3} + {x^2} - 5x + 6\).
b) Đa thức \(A\left( x \right)\) có bậc là 3 và hệ số cao nhất là 1.
c) \(M\left( x \right) = A\left( x \right) - B\left( x \right)\)
\(M\left( x \right) = \left( {{x^3} + {x^2} - 2x - 4} \right) - \left( {{x^3} + {x^2} - 5x + 6} \right)\)
\( = {x^3} + {x^2} - 2x - 4 - {x^3} - {x^2} + 5x - 6\)
\( = \left( {{x^3} - {x^3}} \right) + \left( {{x^2} - {x^2}} \right) + \left( { - 2x + 5x} \right) + \left( { - 4 - 6} \right)\)
\( = 3x - 10\)
Ta có \(M\left( x \right) = 0\) tức là \(3x - 10 = 0\), suy ra \(x = \frac{{10}}{3}\).
Vậy đa thức \(M\left( x \right)\) có nghiệm là \(x = \frac{{10}}{3}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
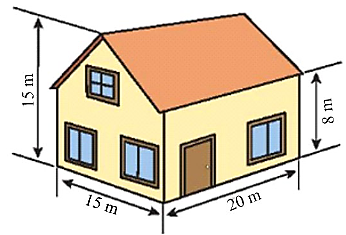
a) Phần thể tích ngôi nhà bằng tổng thể tích phần hình hộp chữ nhật có kích thước \({\rm{20 m}}{\rm{, 15 m}}{\rm{, 8 m}}\)và hình lăng trụ đứng tam giác có kích thước chiều cao là \(20{\rm{ m}}\), cạnh đáy là \({\rm{15 m}}{\rm{,}}\) chiều cao đáy là \({\rm{7 m}}\).
Vậy thể tích phần không gian được giới hạn bởi ngôi nhà là:
\(15.20.8 + \frac{1}{2}.7.15.20 = 3{\rm{ }}450{\rm{ }}\left( {{{\rm{m}}^3}} \right)\)
b) Diện tích xung quanh của ngôi nhà là: \(2\left( {15 + 20} \right).8 + 2.\frac{1}{2}.7.15 = 665{\rm{ }}\left( {{{\rm{m}}^2}} \right)\).
Diện tích tường cần sơn là: \(665 - 25 = 640\) (m2)
Số lít sơn cần mua là: \(640:8 = 80\) (lít)
Lời giải
|
a) Xét \(\Delta ADB\) và \(\Delta AEC\) có: \(\widehat {ADB} = \widehat {AEC} = 90^\circ \); \(AB = AC\) (do \(\Delta ABC\) cân tại \(A\)); \(\widehat {BAC}\) là góc chung. Do đó \(\Delta ADB = \Delta AEC\) (cạnh huyền – góc nhọn). Suy ra \(AD = AE\) (hai cạnh tương ứng). Mà \(AB = AC\) (chứng minh trên) Nên \(AB - AE = AC - AD\) hay \(BE = CD\).
|
 |
b) Do \(\Delta ADB = \Delta AEC\) (câu a) nên \(\widehat {ABD} = \widehat {ACE}\) (hai góc tương ứng)
Xét \(\Delta BHE\) và \(\Delta CHD\) có:
\(\widehat {BEH} = \widehat {CDH} = 90^\circ \);
\(BE = CD\) (chứng minh câu a);
\(\widehat {EBH} = \widehat {DCH}\)(chứng minh trên).
Do đó \(\Delta BHE = \Delta CHD\) (cạnh góc vuông – góc nhọn kề)
Suy ra \(HB = HC\) (hai cạnh tương ứng)
Tam giác \(HBC\) có \(HB = HC\) nên là tam giác cân tại \(H\).
Xét \(\Delta HDC\) vuông tại \(D\) có \(HC\) là cạnh huyền nên là cạnh có độ dài lớn nhất.
Do đó \(HC > HD\).
Mà \(HB = HC\) (chứng minh trên) nên \(HB > HD.\)
c) Gọi \[P\] là giao điểm của \[HI\] và \[BC\].
\(\Delta HBC\) có hai đường trung tuyến \[BM\] và \[CN\] cắt nhau tại \[I\].
Do đó \[I\] là trọng tâm của \(\Delta HBC\) nên \[HP\] là đường trung tuyến xuất phát từ đỉnh \[H\] của tam giác.
Mà \(\Delta HBC\) cân tại \(H\) nên đường trung tuyến \[HP\] đồng thời là đường cao của tam giác.
Suy ra \(HP \bot BC\) hay \(HI \bot BC\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
\(\Delta ABC\) có \[H\] là giao điểm của hai đường cao \[BD\] và \[CE\] nên \[H\] là trực tâm của \(\Delta ABC\).
Do đó \(AH \bot BC\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra ba điểm \(A,H,I\) cùng nằm trên một đường thẳng vuông góc với \[BC\] tại \(P\).
Hay ba điểm \(A,H,I\) thẳng hàng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo