(1,5 điểm)
4.1. Cho hình thang cân có độ dài đáy nhỏ bằng \({\rm{4 cm}}\), độ dài đáy lớn gấp đôi độ dài đáy nhỏ. Tính khoảng cách giữa hai đáy của hình thang cân, biết diện tích hình thang cân đó bằng \({\rm{18 c}}{{\rm{m}}^2}\).
4.2. Tính chu vi của tam giác cân có hai cạnh bằng \(3{\rm{ cm}}\) và \(7{\rm{ cm}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
4.1.
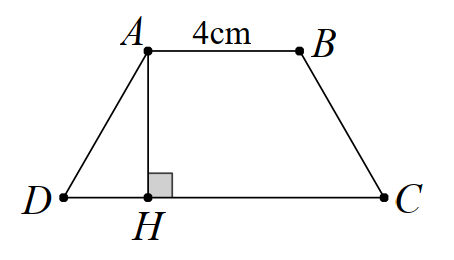
Ta có đáy nhỏ
\(AB = 4{\rm{ cm}}\) và độ dài đáy lớn gấp đôi độ dài của đáy nhỏ.
Do đó độ dài đáy lớn \(CD\) là \(4.2 = 8\) (cm)
Kẻ \(AH \bot CD{\rm{ }}\left( {H \in CD} \right)\), khi đó \(AH\) là chiều cao của hình thang cân \(ABCD.\)
Diện tích của hình thang cân \(ABCD\) bằng \(18{\rm{ c}}{{\rm{m}}^2}\), suy ra \(S = \frac{{\left( {AB + CD} \right).AH}}{2} = 18\).
Mà \(AB = 4{\rm{ cm, }}CD = 8{\rm{ cm}}{\rm{.}}\)
Suy ra \(S = \frac{{\left( {4 + 8} \right).AH}}{2} = 18\).
Vậy chiều cao của hình thang cân là \(AH = \frac{{18.2}}{{4 + 8}} = \frac{{36}}{{12}} = 3\).
4.2. Giả sử tam giác \(ABC\) có \(AB = 3{\rm{ cm, }}AC = 7{\rm{ cm}}{\rm{.}}\)
Theo bất đẳng thức tam giác, ta có: \(\left| {AB - AC} \right| < BC < AB + AC\).
Do đó, \(4 < BC < 10\).
Mà tam giác \(ABC\) cân nên suy ra \(BC = 7{\rm{ cm}}{\rm{.}}\)
Vậy chu vi tam giác \(ABC\) là \(3 + 7 + 7 = 17{\rm{ }}\left( {{\rm{cm}}} \right)\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
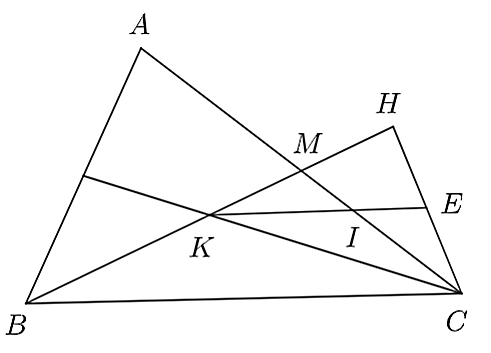
a) Xét \(\Delta HKC\), có:
Ta có: \(BH = 2BK\) hay \(BK + KH = 2BK\) suy ra \(KH = BK.\)
Mà \(MK = \frac{1}{2}KB\) nên \(MK = \frac{1}{2}KH\) hay \(M\) là trung điểm của \(KH\).
Lại có: \(IC = \frac{1}{3}CA = \frac{1}{3}.2MC = \frac{2}{3}MC\) với \(MC\) là trung tuyến của \(\Delta HKC\).
Suy ra \(I\) là trọng tâm của \(\Delta HKC\).
Mà đường thẳng \(KI\) cắt \(HC\) ở \(E\) nên \(E\) là trung điểm của \(HC.\)
b) Ta có \(I\) là trọng tâm của \(\Delta HKC\) nên \(\frac{{IE}}{{KE}} = \frac{2}{3}\) và \(\frac{{IK}}{{KE}} = \frac{1}{3}\) do đó, \(\frac{{IE}}{{IK}} = \frac{1}{2}.\)
Ta có \(\frac{{MI}}{{MC}} = \frac{1}{3}\) hay \(MI = \frac{1}{3}MC\).
Mà \(MC = \frac{1}{2}AC\).
Suy ra \(MI = \frac{1}{3}.\frac{1}{2}AC = \frac{1}{6}AC\).
Do đó, \(\frac{{MI}}{{AC}} = \frac{1}{6}.\)
Lời giải
Hướng dẫn giải
2.1. Gọi giá tiền một gói bạn Huy mua là \(x\) (nghìn đồng)
Vì số tiền mà bạn Tùng và Huy mua đồ là như nhau nên gói bánh, bim bim và giá tiền của nó là hai đại lượng tỉ lệ nghịch.
Do đó, ta có \(12.5 = 6x\) suy ra \(x = \frac{{12.5}}{6} = 10\) (nghìn đồng)
Vậy giá gói bánh bạn Huy mua là 10 nghìn đồng.
2.2. Gọi số sách quyên góp được của ba lớp 7A, 7B, 7C lần lượt là \(x;y;z\) (quyển).
Vì số sách quyên góp được của ba lớp 7A, 7B, 7C lần lượt tỉ lệ với \(16;13;12\) và lớp 7A quyên góp nhiều hơn lớp 7C là 12 quyển nên ta có: \(\frac{x}{{16}} = \frac{y}{{13}} = \frac{z}{{12}}\) và \(x - z = 12\).
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{{16}} = \frac{y}{{13}} = \frac{z}{{12}} = \frac{{x - z}}{{16 - 12}} = \frac{{12}}{4} = 3\)
Suy ra \(\frac{x}{{16}} = 3\) nên \(x = 48\); \(\frac{y}{{13}} = 3\) nên \(y = 39\); \(\frac{z}{{12}} = 3\) nên \(z = 36\).
Vậy số sách quyên góp được của ba lớp 7A, 7B, 7C lần lượt là \(48\) quyển, \(39\) quyển, \(36\) quyển.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo