(0,5 điểm) Chứng minh rằng nếu \(\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}}{\rm{ }}\left( {c + d \ne 0} \right)\) thì \(a = c\) hoặc \(a + b + c + d = 0\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Vì \(\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}}\) nên \(\frac{{a + b}}{{c + d}} = \frac{{c + b}}{{d + a}}\).
Suy ra \(\frac{{a + b}}{{c + d}} + 1 = \frac{{c + b}}{{d + a}} + 1\).
Do đó \(\frac{{a + b}}{{c + d}} + \frac{{c + d}}{{c + d}} = \frac{{c + b}}{{d + a}} + \frac{{d + a}}{{d + a}}\) hay \(\frac{{a + b + c + d}}{{c + d}} = \frac{{c + b + d + a}}{{d + a}}\) (*)
Nếu \(a + b + c + d \ne 0\) nên từ (*) suy ra \(a + d = c + d\) suy ra \(a = c.\)
Nếu \(a + b + c + d = 0\) thì ta có tỉ lệ thức luôn đúng (\(a\) có thể bằng hoặc không bằng \(c\))
Vậy nếu \(\frac{{a + b}}{{b + c}} = \frac{{c + d}}{{d + a}}{\rm{ }}\left( {c + d \ne 0} \right)\) thì \(a = c\) hoặc \(a + b + c + d = 0\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
4.1.
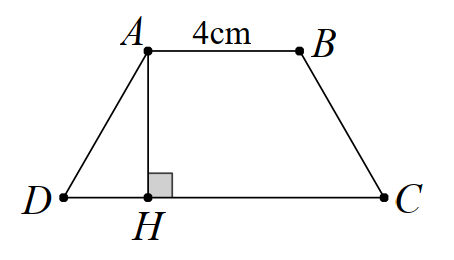
Ta có đáy nhỏ
\(AB = 4{\rm{ cm}}\) và độ dài đáy lớn gấp đôi độ dài của đáy nhỏ.
Do đó độ dài đáy lớn \(CD\) là \(4.2 = 8\) (cm)
Kẻ \(AH \bot CD{\rm{ }}\left( {H \in CD} \right)\), khi đó \(AH\) là chiều cao của hình thang cân \(ABCD.\)
Diện tích của hình thang cân \(ABCD\) bằng \(18{\rm{ c}}{{\rm{m}}^2}\), suy ra \(S = \frac{{\left( {AB + CD} \right).AH}}{2} = 18\).
Mà \(AB = 4{\rm{ cm, }}CD = 8{\rm{ cm}}{\rm{.}}\)
Suy ra \(S = \frac{{\left( {4 + 8} \right).AH}}{2} = 18\).
Vậy chiều cao của hình thang cân là \(AH = \frac{{18.2}}{{4 + 8}} = \frac{{36}}{{12}} = 3\).
4.2. Giả sử tam giác \(ABC\) có \(AB = 3{\rm{ cm, }}AC = 7{\rm{ cm}}{\rm{.}}\)
Theo bất đẳng thức tam giác, ta có: \(\left| {AB - AC} \right| < BC < AB + AC\).
Do đó, \(4 < BC < 10\).
Mà tam giác \(ABC\) cân nên suy ra \(BC = 7{\rm{ cm}}{\rm{.}}\)
Vậy chu vi tam giác \(ABC\) là \(3 + 7 + 7 = 17{\rm{ }}\left( {{\rm{cm}}} \right)\).
Lời giải
Hướng dẫn giải
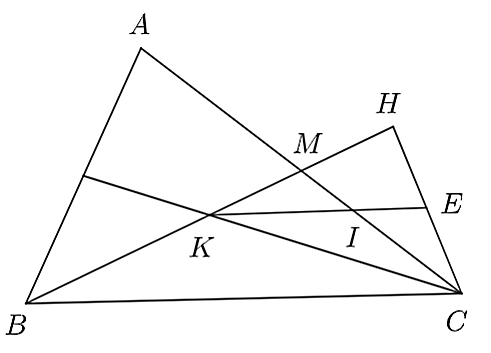
a) Xét \(\Delta HKC\), có:
Ta có: \(BH = 2BK\) hay \(BK + KH = 2BK\) suy ra \(KH = BK.\)
Mà \(MK = \frac{1}{2}KB\) nên \(MK = \frac{1}{2}KH\) hay \(M\) là trung điểm của \(KH\).
Lại có: \(IC = \frac{1}{3}CA = \frac{1}{3}.2MC = \frac{2}{3}MC\) với \(MC\) là trung tuyến của \(\Delta HKC\).
Suy ra \(I\) là trọng tâm của \(\Delta HKC\).
Mà đường thẳng \(KI\) cắt \(HC\) ở \(E\) nên \(E\) là trung điểm của \(HC.\)
b) Ta có \(I\) là trọng tâm của \(\Delta HKC\) nên \(\frac{{IE}}{{KE}} = \frac{2}{3}\) và \(\frac{{IK}}{{KE}} = \frac{1}{3}\) do đó, \(\frac{{IE}}{{IK}} = \frac{1}{2}.\)
Ta có \(\frac{{MI}}{{MC}} = \frac{1}{3}\) hay \(MI = \frac{1}{3}MC\).
Mà \(MC = \frac{1}{2}AC\).
Suy ra \(MI = \frac{1}{3}.\frac{1}{2}AC = \frac{1}{6}AC\).
Do đó, \(\frac{{MI}}{{AC}} = \frac{1}{6}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.