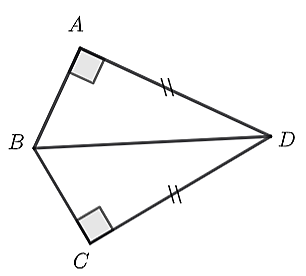
Cho hình vẽ bên. Khi đó, \(\Delta ABD = \Delta DBC\) theo trường hợp
A. Cạnh góc vuông – góc nhọn kề.
B. Cạnh – góc – cạnh.
C. Góc vuông – cạnh góc vuông.
D. Cạnh huyền – cạnh góc vuông.
Quảng cáo
Trả lời:
Đáp án đúng là: D
Xét \(\Delta ABD\) và \(\Delta DBC\) có: \(AD = DC\) (gt) và \(DB\) là cạnh chung.
Do đó, \(\Delta ABD = \Delta DBC\)(cạnh huyền – cạnh góc vuông)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 8 (chương trình mới) ( 120.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
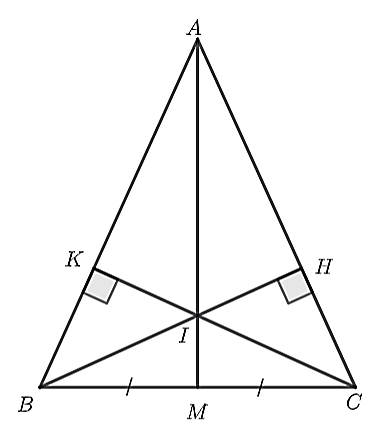
a) Xét \(\Delta ABH\) và \(\Delta ACK\), có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(\widehat {BHA} = \widehat {CKA} = 90^\circ \) (giả thiết)
\(\widehat {KAC} = \widehat {HAB}\) \(\left( { = \widehat {BAC}} \right)\)
Do đó, \(\Delta ABH = \Delta ACK\) (ch – gn).
b) Từ câu a), ta có: \(\Delta ABH = \Delta ACK\) nên \(\widehat {ABH} = \widehat {ACK}\) (hai góc tương ứng)
Lại có, \(\widehat {ABC} = \widehat {ACB}\) (\(\Delta ABC\) cân tại \(A\)).
Ta có: \(\widehat {ABC} = \widehat {ABH} + \widehat {HBC}\)
\(\widehat {ACB} = \widehat {ACK} + \widehat {KCB}\)
Suy ra \(\widehat {HBC} = \widehat {KCB}\) nên \(\Delta BIC\) cân tại \(I\) nên \(IB = IC.\)
c) Từ a) ta có \(\Delta ABH = \Delta ACK\) (ch – gn) nên \(AH = AK\) (hai cạnh tương ứng)
Xét \(\Delta KAI\) và \(\Delta HAI\) có:
\(AI\) chung (giả thiết)
\(AH = AK\) (cmt)
Suy ra \(\Delta KAI = \Delta HAI\) (ch – cgv)
Do đó, \(\widehat {KAI} = \widehat {HAI}\) (hai góc tương ứng)
Suy ra \(AI\) là tia phân giác của \(\widehat {BAC}\) (1)
Xét \(\Delta ABM\) và \(\Delta ACM,\) có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(\widehat {ABC} = \widehat {ACB}\)(\(\Delta ABC\) cân tại \(A\))
\(AM = MB\) (gt)
Do đó, \(\Delta ABM = \Delta ACM\) (c.g.c)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) (hai góc tương ứng)
Suy ra \(AM\) là tia phân giác của \(\widehat {BAC}\) (2)
Từ (1) và (2) suy ra \(A,I,M\) thẳng hàng.
Lời giải
Hướng dẫn giải
Đáp án: \(400\)
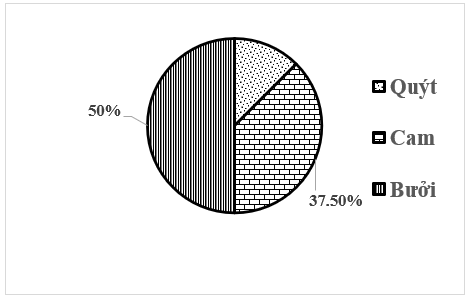
Tỉ lệ phần trăm số cây quýt trồng trong vườn nhà ông Quang là: \(100\% - 50\% - 37,5\% = 12,5\% \).
Mà ta có số cây quýt trồng trong vườn là 50 cây.
Do đó, tổng số cây ăn quả được trồng trong vườn nhà ông Quang là: \(50:12,5.100 = 400\) (cây).
Vậy trong vườn có 400 cây ăn quả.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{2}{4}.\)
B. \(\frac{6}{{18}}.\)
C. \(\frac{2}{9}.\)
D. \(\frac{{ - 3}}{9}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.