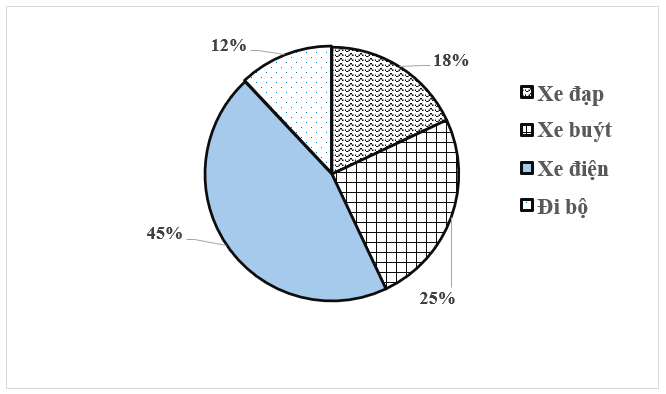
Trong vườn nhà ông Quang trồng ba loại cây ăn quả: Cam, Quýt, Bưởi với tỉ lệ được biểu diễn như biểu đồ dưới đây.
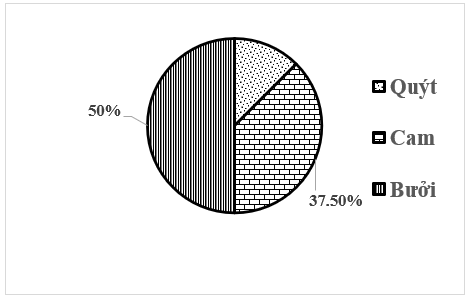
Biết rằng, trong vườn trồng \(50\) cây quýt. Hỏi tổng số cây ăn quả trong vườn nhà ông Quang là bao nhiêu?
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: \(400\)
Tỉ lệ phần trăm số cây quýt trồng trong vườn nhà ông Quang là: \(100\% - 50\% - 37,5\% = 12,5\% \).
Mà ta có số cây quýt trồng trong vườn là 50 cây.
Do đó, tổng số cây ăn quả được trồng trong vườn nhà ông Quang là: \(50:12,5.100 = 400\) (cây).
Vậy trong vườn có 400 cây ăn quả.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
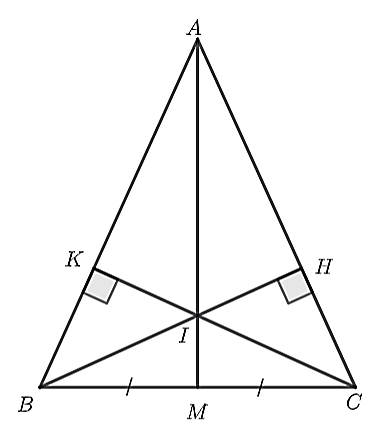
a) Xét \(\Delta ABH\) và \(\Delta ACK\), có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(\widehat {BHA} = \widehat {CKA} = 90^\circ \) (giả thiết)
\(\widehat {KAC} = \widehat {HAB}\) \(\left( { = \widehat {BAC}} \right)\)
Do đó, \(\Delta ABH = \Delta ACK\) (ch – gn).
b) Từ câu a), ta có: \(\Delta ABH = \Delta ACK\) nên \(\widehat {ABH} = \widehat {ACK}\) (hai góc tương ứng)
Lại có, \(\widehat {ABC} = \widehat {ACB}\) (\(\Delta ABC\) cân tại \(A\)).
Ta có: \(\widehat {ABC} = \widehat {ABH} + \widehat {HBC}\)
\(\widehat {ACB} = \widehat {ACK} + \widehat {KCB}\)
Suy ra \(\widehat {HBC} = \widehat {KCB}\) nên \(\Delta BIC\) cân tại \(I\) nên \(IB = IC.\)
c) Từ a) ta có \(\Delta ABH = \Delta ACK\) (ch – gn) nên \(AH = AK\) (hai cạnh tương ứng)
Xét \(\Delta KAI\) và \(\Delta HAI\) có:
\(AI\) chung (giả thiết)
\(AH = AK\) (cmt)
Suy ra \(\Delta KAI = \Delta HAI\) (ch – cgv)
Do đó, \(\widehat {KAI} = \widehat {HAI}\) (hai góc tương ứng)
Suy ra \(AI\) là tia phân giác của \(\widehat {BAC}\) (1)
Xét \(\Delta ABM\) và \(\Delta ACM,\) có:
\(AB = AC\) (\(\Delta ABC\) cân tại \(A\))
\(\widehat {ABC} = \widehat {ACB}\)(\(\Delta ABC\) cân tại \(A\))
\(AM = MB\) (gt)
Do đó, \(\Delta ABM = \Delta ACM\) (c.g.c)
Suy ra \(\widehat {BAM} = \widehat {CAM}\) (hai góc tương ứng)
Suy ra \(AM\) là tia phân giác của \(\widehat {BAC}\) (2)
Từ (1) và (2) suy ra \(A,I,M\) thẳng hàng.
Lời giải
Hướng dẫn giải
Nhận thấy \({\left( {x - 3} \right)^2} \ge 0\) suy ra \(\sqrt {{{\left( {x - 3} \right)}^2}} \ge 0\) với mọi \(x\),
\({\left( {y + 3} \right)^2} \ge 0\) suy ra \(\sqrt {{{\left( {y + 3} \right)}^2}} \ge 0\) với mọi \(y\),
\(\left| {x + y + z} \right| \ge 0\).
Do đó, \(\sqrt {{{\left( {x - 3} \right)}^2}} + \sqrt {{{\left( {y + 3} \right)}^2}} + \left| {x + y + z} \right| \ge 0\).
Để \(\sqrt {{{\left( {x - 3} \right)}^2}} + \sqrt {{{\left( {y + 3} \right)}^2}} + \left| {x + y + z} \right| = 0\) thì đồng thời \(\sqrt {{{\left( {x - 3} \right)}^2}} = 0,\) \(\sqrt {{{\left( {y + 3} \right)}^2}} = 0\) và \(\left| {x + y + z} \right| = 0\).
• Giải \(\sqrt {{{\left( {x - 3} \right)}^2}} = 0\) ta có: \({\left( {x - 3} \right)^2} = 0\), suy ra \(x - 3 = 0\) hay \(x = 3\) (thỏa mãn).
• Giải \(\sqrt {{{\left( {y + 3} \right)}^2}} = 0\) ta có: \({\left( {y + 3} \right)^2} = 0\), suy ra \(y + 3 = 0\) hay \(y = - 3\) (thỏa mãn).
• Giải \(\left| {x + y + z} \right| = 0\), ta có: \(x + y + z = 0\).
Mà \(x = 3\) và \(y = - 3\) nên ta có \(3 + \left( { - 3} \right) + z = 0\) hay \(z + 0 = 0\) suy ra \(z = 0\).
Vậy \(x = 3,\)\(y = - 3\) và \(z = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{2}{4}.\)
B. \(\frac{6}{{18}}.\)
C. \(\frac{2}{9}.\)
D. \(\frac{{ - 3}}{9}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.