Trong định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” có phần giả thiết là
A. “Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba”.
B. “Chúng song song với nhau”.
C. “Hai đường thẳng phân biệt cùng vuông góc”.
D. “Hai đường thẳng phân biệt”.
Quảng cáo
Trả lời:
Đáp án đúng là: A
Phần giải thiết của định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là ‘Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba”.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
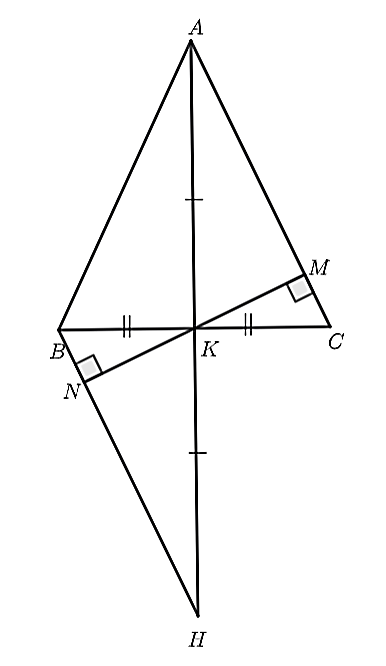
a) Xét \(\Delta AKC\) và \(\Delta AKB,\) có:
\(AB = AC\) (gt)
\(BK = KC\)(gt)
\(AK\) chung
Do đó, \(\Delta AKC = \Delta AKB\) (c.c.c)
b) Vì \(\Delta AKC = \Delta AKB\) (cmt) nên \(\widehat {ABK} = \widehat {ACK}\) (hai góc tương ứng) và \(\widehat {AKB} = \widehat {AKC} = 90^\circ \) (hai góc tương ứng)
Xét \(\Delta AKB\) và \(\Delta HKB\), có:
\(BK\) chung
\(AH = HK\)
\(\widehat {AKB} = \widehat {BKH} = 90^\circ \)
Do đó, \(\Delta AKB = \Delta HKB\) (c.g.c)
Suy ra \(\widehat {ABK} = \widehat {HBK}\) (hai cạnh tương ứng).
Mà \(\widehat {ABK} = \widehat {ACK}\) nên \(\widehat {HBK} = \widehat {ACK}\).
Mà hai góc ở vị trí so le trong nên \(BH\parallel AC\).
c) Xét \(\Delta NKH\) và \(\Delta MKA\), có:
\(AK = KH\) (gt)
\(\widehat {KNH} = \widehat {KMA} = 90^\circ \)
\(\widehat {NHK} = \widehat {KAM}\) (so le trong)
Do đó, \(\Delta NKH = \Delta MKA\) (cgv – gn)
Suy ra \(\widehat {NKH} = \widehat {AKM}\) (hai góc tương ứng)
Lại có, \(\widehat {NKH} + \widehat {NKA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {NKA} + \widehat {AKM} = 180^\circ \) hay \(\widehat {NKM} = 180^\circ \).
Vậy ba điểm \(N,K,M\) thẳng hàng.
Câu 2
A. \(25,3.\)
B. \(25,33.\)
C. \(25,32.\)
D. \(25,325.\)
Lời giải
Đáp án đúng là: A
Làm tròn số \(35,3256\) với độ chính xác \(0,05\) (hay làm tròn đến phần mười) được \(25,3.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 0.
B. 1.
C. 2.
D. 3.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.