Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \[\left( { - 2 \le x \le 2} \right)\], mặt cắt là tam giác vuông có một góc và độ dài một cạnh góc vuông là \[\sqrt {4 - {x^2}} \] (dm) như hình vẽ. Tính thể tích của vật thể.
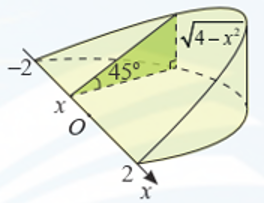
Khi cắt một vật thể hình chiếc niêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \[\left( { - 2 \le x \le 2} \right)\], mặt cắt là tam giác vuông có một góc và độ dài một cạnh góc vuông là \[\sqrt {4 - {x^2}} \] (dm) như hình vẽ. Tính thể tích của vật thể.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Vì mặt cắt là tam giác vuông có một góc 450 nên mặt cắt là tam giác vuông cân.
Do đó diện tích của mặt cắt là: \(S(x) = \frac{1}{2}{\left( {\sqrt {4 - {x^2}} } \right)^2} = \frac{1}{2}\left( {4 - {x^2}} \right) = 2 - \frac{1}{2}{x^2}\)
Thể tích vật thể là: \(V = \int_{ - 2}^2 {\left( {2 - \frac{1}{2}{x^2}} \right)} dx = \left. {\left( {2x - \frac{{{x^3}}}{6}} \right)} \right|_{ - 2}^2 = \frac{8}{3} + \frac{8}{3} = \frac{{16}}{3}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
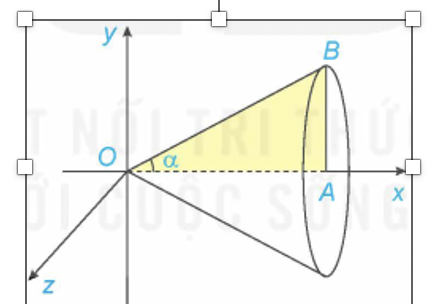
a) Xét tam giác OAB vuông tại A , có \({\rm{AB}} = {\rm{OA}}\). tana = a.tana.
Khi quay miền tam giác OAB xung quanh trục Ox ta được khối nón có bán kính đáy \({\rm{r}} = {\rm{AB}} = {\rm{a}}\).tana và chiều cao \({\rm{h}} = {\rm{OA}} = {\rm{a}}\).
Do đó \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {a^3}{\tan ^2}\alpha \)
b) Có \({V^\prime } = \frac{1}{3}\pi {a^3} \cdot 2\tan \alpha \cdot \frac{1}{{{{\cos }^2}\alpha }}\)
Vi \(0 < \alpha \le \frac{\pi }{4} = > 0 < \) tan \(\alpha \le 1\) nên \({V^\prime } > 0\). Do đó \(V\) là hàm số đồng biến trên \(\left( {0;\frac{\pi }{4}} \right)\)
Do đó \(\mathop {\max }\limits_{\left( {0;\frac{\pi }{4}} \right]} V = V\left( {\frac{\pi }{4}} \right) = \frac{1}{3}\pi {a^3}\)
Vậy \(\alpha = \frac{\pi }{4}\) thì thể tích khối nón là lớn nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
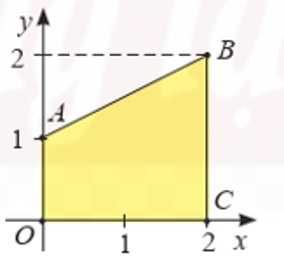
Ta có OABC là hình thang vuông, có đường cao OC nằm trên trục Ox .
Khi quay hình thang OABC quanh trục Ox ta được khối tròn xoay là khối nón cụt, có bán kính đáy bé \({r_1} = OA = 1\), bán kính đáy lớn \({r_2} = BC = 2\) và chiều cao \(h\) \( = OC = 2\).
Thể tích cần tính là: \(V = \frac{1}{3}\pi \left( {r_1^2 + {r_1}{r_2} + r_2^2} \right)h = \frac{1}{3}\pi \left( {{1^2} + 1 \cdot 2 + {2^2}} \right) \cdot 2 = \frac{{14\pi }}{3}\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập