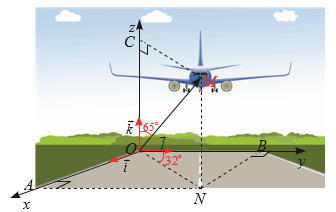
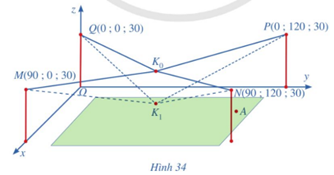
Ở một sân bay, ví trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình vẽ bên dưới. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy).
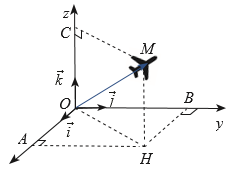
Cho biết OM = 50, \[\left( {\overrightarrow i {\rm{, }}\overrightarrow {OH} } \right) = {64^ \circ },\left( {\overrightarrow {OH} {\rm{, }}\overrightarrow {OM} } \right) = {48^ \circ }\]. Tìm toạ độ của điểm M.
Cho biết OM = 50, \[\left( {\overrightarrow i {\rm{, }}\overrightarrow {OH} } \right) = {64^ \circ },\left( {\overrightarrow {OH} {\rm{, }}\overrightarrow {OM} } \right) = {48^ \circ }\]. Tìm toạ độ của điểm M.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Giả sử \({\rm{M}}({\rm{x}};{\rm{y}};{\rm{z}})\).
\({\rm{H}} \in ({\rm{Oxy}}) \Rightarrow {\rm{H}}({\rm{x}};{\rm{y}};0){\rm{. }}\)
Vì OBHA là hình bình hành nên \({\rm{BH}} = {\rm{OA}}\).
Vì \({\rm{OCMH}}\) là hình bình hành nên \({\rm{OC}} = {\rm{MH}}\).
Xét vuông tại \({\rm{H}}\), có .
Xét vuông tại \({\rm{A}}\), có
Xét vuông tại B, có \(OB = \sqrt {O{H^2} - B{H^2}} = \sqrt {{{33,46}^2} - {{14,67}^2}} \approx 30,07\).
Vì \(\overrightarrow {OA} \) và \(\vec i\) cùng hướng và \({\rm{OA}} = 14,67\) nên \(\overrightarrow {OA} = 14,67\vec i\).
Vì \(\overrightarrow {OB} \) và \(\vec j\) cùng hướng và \({\rm{OB}} = 30,07\) nên \(\overrightarrow {OB} = 30,07\vec j\).
Vì \(\overrightarrow {OC} \) và \(\vec k\) cùng hướng và \(OC = 37,16\) nên \(\overrightarrow {OC} = 37,16\vec k\).
Áp dụng quy tắc hình bình hành, ta có:
\(\overrightarrow {OM} = \overrightarrow {OH} + \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 14,67\vec i + 30,07\vec j + 27,16\vec k\)
Vậy \({\rm{M}}(14,67;30,07;27,16)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
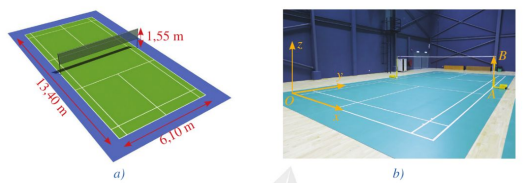
Gọi tọa độ điểm \(A\) là \(\left( {{x_A};{y_A};{z_A}} \right)\). Vì chiểu rộng của sân là \(6,1\;{\rm{m}}\) nên \({x_A} = 6,1\). Do một nửa chiều dài của sân là \(6,7\;{\rm{m}}\) nên \({y_A} = 6,7\). Điểm \(A\) thuộc mặt phẳng \((Oxy)\) nên \({z_A} = 0\). Vì vậy, điểm \(A\) có tọa độ là \((6,1;6,7;0)\).
Độ dài đoạn thẳng AB là \(1,55\;{\rm{m}}\) nên điểm \(B\) có toạ độ là \((6,1;6,7;1,55)\).
Vậy ta có: \(\overrightarrow {AB} = (6,1 - 6,1;6,7 - 6,7;1,55 - 0)\), tức là \(\overrightarrow {AB} = (0;0;1,55)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Quāng đường máy bay bay được với vận tốc \(890\;{\rm{km}}/{\rm{h}}\) trong nửa giờ là: \(890 \cdot \frac{1}{2} = 445(\;{\rm{km}})\). Vì máy bay duy trì hướng bay về phía nam nên tọa độ của vectơ biểu diễn độ dịch chuyển của chiếc máy bay trong nứa giờ đó với hệ tọa độ đã chọn là \((0;445;0)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập