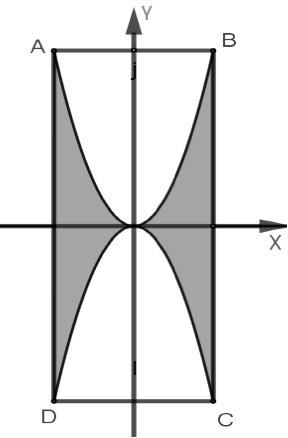
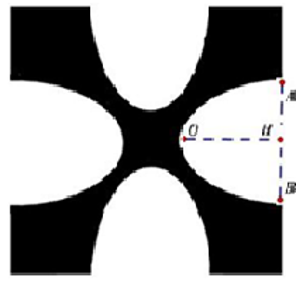
Một viên gạch hoa hình vuông cạnh \(40{\rm{cm}}\). Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ dưới).
Diện tích mỗi cánh hoa của viên gạch bằng
Một viên gạch hoa hình vuông cạnh \(40{\rm{cm}}\). Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô đen như hình vẽ dưới).
Diện tích mỗi cánh hoa của viên gạch bằng
A. \(800\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
B. \[\frac{{800}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
C. \(\frac{{400}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
D. \(250\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn C
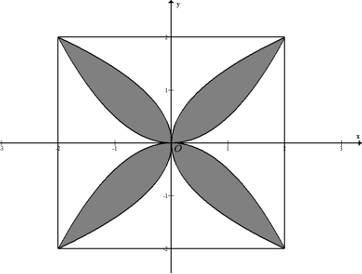
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng \(10cm = 1dm\)), các cánh hoa tạo bởi các đường parabol có phương trình \(y = \frac{{{x^2}}}{2}\), \(y = - \frac{{{x^2}}}{2}\),\(x = - \frac{{{y^2}}}{2}\),\(x = \frac{{{y^2}}}{2}\).
Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi hai đồ thị hàm số\(y = \frac{{{x^2}}}{2}\),\(y = \sqrt {2x} \) và hai đường thẳng \(x = 0;x = 2\).
Do đó diện tích một cánh hoa bằng
\(\int\limits_0^2 {\left( {\sqrt {2x} - \frac{{{x^2}}}{2}} \right){\rm{d}}x} \) \[ = \left. {\left. {\left( {\frac{{2\sqrt 2 }}{3}\sqrt {{{\left( {2x} \right)}^3}} - \frac{{{x^3}}}{6}} \right)} \right|} \right|_0^2\]\[ = \frac{4}{3}\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right) = \frac{{400}}{3}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\]\[ = \frac{4}{3}\left( {{\rm{d}}{{\rm{m}}^{\rm{2}}}} \right) = \frac{{400}}{3}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.105660667đ
B.1066666667đ
C.107665667đ
D.108665667đ
Lời giải
Chọn B
Vì \(AB = 4dm;BC = 8dm.\)\( \Rightarrow A( - 2;4),\)\(B(2;4),C(2; - 4),D( - 2; - 4)\).
parabol là: \(y = {x^2}\) hoặc \(y = - {x^2}\)
Diện tích phần tô đậm là \[{S_1} = 4\int\limits_0^2 {{x^2}dx = \frac{{32}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})} \]
Diện tích hình chữ nhật là \[S = 4.8 = 32\begin{array}{*{20}{c}}{}\end{array}({m^2})\]
Diện tích phần trắng là \[{S_2} = S - {S_1} = 32 - \frac{{32}}{3} = \frac{{64}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})\]
Tổng chi phí trang chí là:
Câu 2
A. \(110\) triệu đồng.
B. \(250\) triệu đồng.
C. \(180\) triệu đồng.
D. \(200\) triệu đồng.
Lời giải
Chọn D
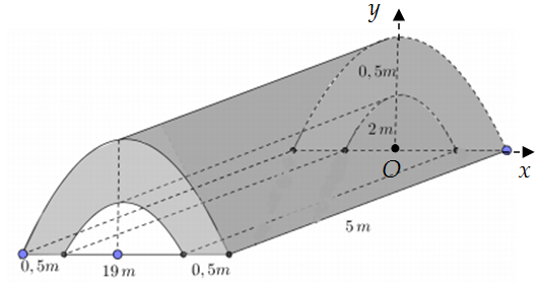
Chọn hệ trục \[Oxy\] như hình vẽ.
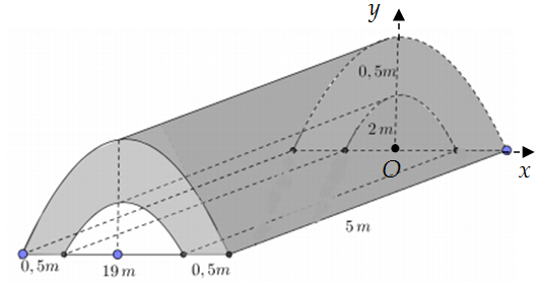
Gọi \[\left( {{P_1}} \right):y = {a_1}{x^2} + {b_1}\] là Parabol đi qua hai điểm \[A\left( {\frac{{19}}{2};0} \right),B\left( {0;2} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = a.{\left( {\frac{{19}}{2}} \right)^2} + 2\\2 = b\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = - \frac{8}{{361}}\\{b_1} = 2\end{array} \right.\]\[ \Rightarrow \left( {{P_1}} \right):y = - \frac{8}{{361}}{x^2} + 2\].
Gọi \[\left( {{P_2}} \right):y = {a_2}{x^2} + {b_2}\] là Parabol đi qua hai điểm \[C\left( {10;0} \right),D\left( {0;\frac{5}{2}} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = {a_2}.{\left( {10} \right)^2} + \frac{5}{2}\\\frac{5}{2} = {b_2}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_2} = - \frac{1}{{40}}\\{b_2} = \frac{5}{2}\end{array} \right.\]\[ \Rightarrow \left( {{P_2}} \right):y = - \frac{1}{{40}}{x^2} + \frac{5}{2}\].
Ta có thể tích của bê tông là: \[V = 5.2\left[ {\int_0^{10} {\left( { - \frac{1}{{40}}{x^2} + \frac{5}{2}} \right)} {\rm{d}}x - \int_0^{\frac{{19}}{2}} {\left( { - \frac{8}{{361}}{x^2} + 2} \right)} {\rm{d}}x} \right] = 40\,{{\rm{m}}^3}\].
Số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu là: \[5.40 = 200\] triệu đồng
Câu 3
A. \[11445000\] đồng.
B. \[4077000\] đồng.
C. \[7368000\] đồng.
D. \[11370000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[{V_1} = \frac{{2\sqrt 3 {R^3}}}{9}\].
B. \[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{27}}\].
C. \[{V_1} = \frac{{\sqrt 3 \pi {R^3}}}{{18}}\].
D. \[{V_1} = \frac{{\sqrt 3 {R^3}}}{{27}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(30\;{m^3}\)
B. \(36\;{m^3}\)
C. \(40\;{m^3}\)
D. \(41\;{m^3}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập