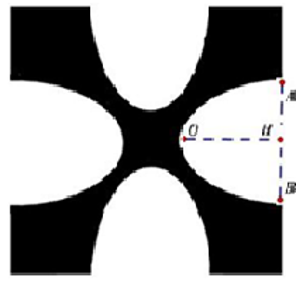
Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng\[R\]. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc \[{30^0}\] ta thu được hai khối gỗ có thể tích là \[{V_1}\] và \[{V_2}\], với \[{V_1} < {V_2}\]. Thể tích \[{V_1}\] bằng?

Cho một vật thể bằng gỗ có dạng hình trụ với chiều cao và bán kính đáy cùng bằng\[R\]. Cắt khối gỗ đó bởi một mặt phẳng đi qua đường kính của một mặt đáy của khối gỗ và tạo với mặt phẳng đáy của khối gỗ một góc \[{30^0}\] ta thu được hai khối gỗ có thể tích là \[{V_1}\] và \[{V_2}\], với \[{V_1} < {V_2}\]. Thể tích \[{V_1}\] bằng?

A. \[{V_1} = \frac{{2\sqrt 3 {R^3}}}{9}\].
Quảng cáo
Trả lời:
Chọn A
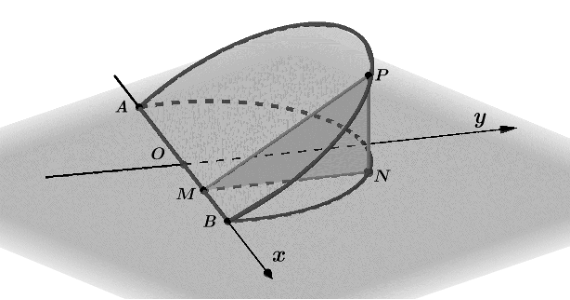
Khi cắt khối gỗ hình trụ ta được một hình nêm có thể tích \[{V_1}\] như hình vẽ.
Chọn hệ trục tọa độ \[Oxy\] như hình vẽ.
Nửa đường tròn đường kính \[AB\] có phương trình là \[y = \sqrt {{R^2} - {x^2}} \],\[x \in \left[ { - R;R} \right]\].
Một mặt phẳng vuông góc với trục \[Ox\] tại điểm \[M\] có hoành độ \[x\], cắt hình nêm theo thiết diện là \[\Delta MNP\] vuông tại \[N\] và có \[\widehat {PMN} = {30^0}\].
Ta có \[NM = y = \sqrt {{R^2} - {x^2}} \Rightarrow NP = MN.\tan {30^0} = \frac{{\sqrt {{R^2} - {x^2}} }}{{\sqrt 3 }}\].
\[\Delta MNP\] có diện tích \[S\left( x \right) = \frac{1}{2}NM.NP = \frac{1}{2}.\frac{{{R^2} - {x^2}}}{{\sqrt 3 }}\].
Thể tích hình nêm là \[{V_1} = \int\limits_{ - R}^R {S\left( x \right)} {\rm{d}}x = \frac{1}{2}\int\limits_{ - R}^R {\frac{{{R^2} - {x^2}}}{{\sqrt 3 }}} {\rm{d}}x\]\[ = \frac{1}{{2\sqrt 3 }}\left. {\left( {{R^2}x - \frac{1}{3}{x^3}} \right)} \right|_{ - R}^R = \frac{{2\sqrt 3 {R^3}}}{9}\].
* Chú ý: Có thể ghi nhớ công thức tính thể tích hình nêm:
\[{V_1} = \frac{2}{3}{R^2}h = \frac{2}{3}{R^3}\tan \alpha \], trong đó \[R = \frac{{AB}}{2}\], \[\alpha = \widehat {PMN}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.105660667đ
B.1066666667đ
C.107665667đ
D.108665667đ
Lời giải
Chọn B
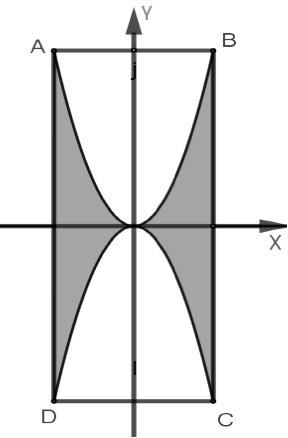
Vì \(AB = 4dm;BC = 8dm.\)\( \Rightarrow A( - 2;4),\)\(B(2;4),C(2; - 4),D( - 2; - 4)\).
parabol là: \(y = {x^2}\) hoặc \(y = - {x^2}\)
Diện tích phần tô đậm là \[{S_1} = 4\int\limits_0^2 {{x^2}dx = \frac{{32}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})} \]
Diện tích hình chữ nhật là \[S = 4.8 = 32\begin{array}{*{20}{c}}{}\end{array}({m^2})\]
Diện tích phần trắng là \[{S_2} = S - {S_1} = 32 - \frac{{32}}{3} = \frac{{64}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})\]
Tổng chi phí trang chí là:
Câu 2
A. \(110\) triệu đồng.
B. \(250\) triệu đồng.
C. \(180\) triệu đồng.
Lời giải
Chọn D
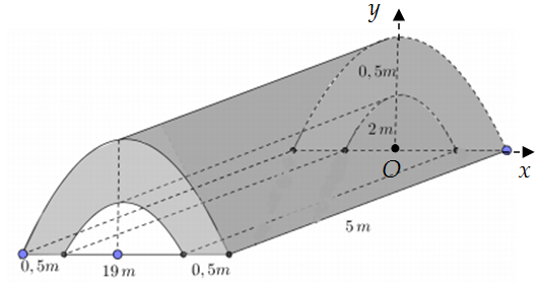
Chọn hệ trục \[Oxy\] như hình vẽ.
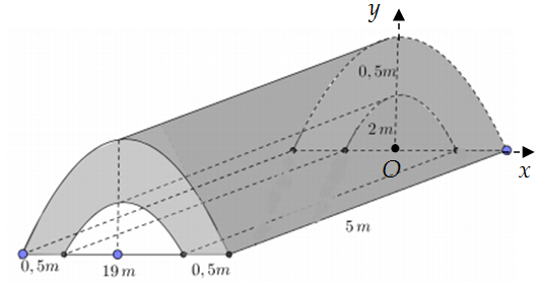
Gọi \[\left( {{P_1}} \right):y = {a_1}{x^2} + {b_1}\] là Parabol đi qua hai điểm \[A\left( {\frac{{19}}{2};0} \right),B\left( {0;2} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = a.{\left( {\frac{{19}}{2}} \right)^2} + 2\\2 = b\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = - \frac{8}{{361}}\\{b_1} = 2\end{array} \right.\]\[ \Rightarrow \left( {{P_1}} \right):y = - \frac{8}{{361}}{x^2} + 2\].
Gọi \[\left( {{P_2}} \right):y = {a_2}{x^2} + {b_2}\] là Parabol đi qua hai điểm \[C\left( {10;0} \right),D\left( {0;\frac{5}{2}} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = {a_2}.{\left( {10} \right)^2} + \frac{5}{2}\\\frac{5}{2} = {b_2}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_2} = - \frac{1}{{40}}\\{b_2} = \frac{5}{2}\end{array} \right.\]\[ \Rightarrow \left( {{P_2}} \right):y = - \frac{1}{{40}}{x^2} + \frac{5}{2}\].
Ta có thể tích của bê tông là: \[V = 5.2\left[ {\int_0^{10} {\left( { - \frac{1}{{40}}{x^2} + \frac{5}{2}} \right)} {\rm{d}}x - \int_0^{\frac{{19}}{2}} {\left( { - \frac{8}{{361}}{x^2} + 2} \right)} {\rm{d}}x} \right] = 40\,{{\rm{m}}^3}\].
Số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu là: \[5.40 = 200\] triệu đồng
Câu 3
A. \[11445000\] đồng.
B. \[4077000\] đồng.
C. \[7368000\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(800\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
B. \[\frac{{800}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\].
C. \(\frac{{400}}{3}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[2553333\] đồng.
B. \[2333333\] đồng.
C. \[2780333\] đồng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.