Có một cốc nước thủy tinh hình trụ, bán kính trong lòng đáy cốc là \(6\,{\rm{cm}}\), chiều cao lòng cốc là \(10\,{\rm{cm}}\) đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng cốc thì đáy mực nước trùng với đường kính đáy.
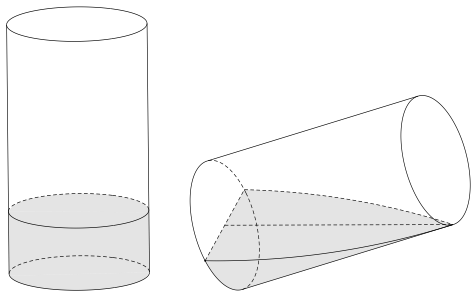
Có một cốc nước thủy tinh hình trụ, bán kính trong lòng đáy cốc là \(6\,{\rm{cm}}\), chiều cao lòng cốc là \(10\,{\rm{cm}}\) đang đựng một lượng nước. Tính thể tích lượng nước trong cốc, biết khi nghiêng cốc nước vừa lúc khi nước chạm miệng cốc thì đáy mực nước trùng với đường kính đáy.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn A
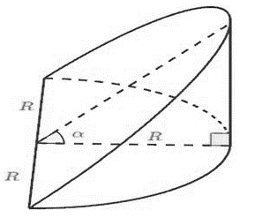
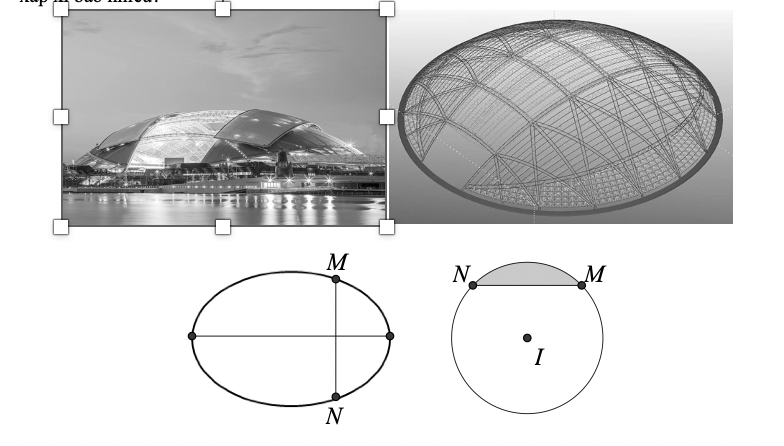
Cách 1. Xét thiết diện cắt cốc thủy tinh vuông góc với đường kính tại vị trí bất kỳ có: \(S\left( x \right) = \frac{1}{2}\sqrt {{R^2} - {x^2}} .\sqrt {{R^2} - {x^2}} .\tan \alpha \) \( \Rightarrow S\left( x \right) = \frac{1}{2}\left( {{R^2} - {x^2}} \right)\tan \alpha \).
Thể tích hình cái nêm là: \(V = \frac{1}{2}\tan \alpha \int\limits_{ - R}^R {\left( {{R^2} - {x^2}} \right)} {\rm{ d}}x = \frac{2}{3}{R^3}\tan \alpha \).
Thể tích khối nước tạo thành khi nguyên cốc có hình dạng cái nêm nên \({V_{kn}} = \frac{2}{3}{R^3}\tan \alpha \). \( \Rightarrow {V_{kn}} = \frac{2}{3}{R^3}.\frac{h}{R} = 240\,{\rm{c}}{{\rm{m}}^{\rm{3}}}\).
Cách 2. Dựng hệ trục tọa độ \[Oxyz\]
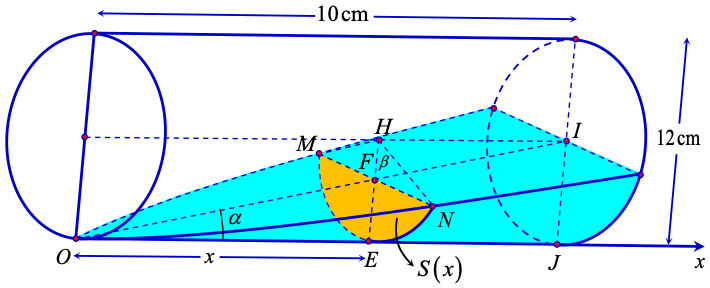
Gọi \[S\left( x \right)\] là diện tích thiết diện do mặt phẳng có phương vuông góc với trục \[Ox\] với khối nước, mặt phẳng này cắt trục \[Ox\] tại điểm có hoành độ \(h \ge x \ge 0\).
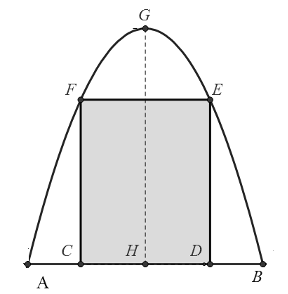
Gọi \(\widehat {IOJ} = \alpha ,\,\widehat {FHN} = \beta ,\,OE = x\)
\(\tan \alpha = \frac{{IJ}}{{OJ}} = \frac{6}{{10}} = \frac{{EF}}{{OE}}\) \( \Rightarrow EF = \frac{{6x}}{{10}}\) \( \Rightarrow HF = 6 - \frac{{6x}}{{10}}\).
\(\cos \beta = \frac{{HF}}{{HN}} = \frac{{6 - \frac{{6x}}{{10}}}}{6} = 1 - \frac{x}{{10}}\); \(\beta = \arccos \left( {1 - \frac{x}{{10}}} \right)\)
\(S\left( x \right) = {S_{\left( {hinh\,quat} \right)}} - {S_{HMN}} = \frac{1}{2}H{N^2}.2\beta - \frac{1}{2}HM.HN.\sin 2\beta \)
\( \Rightarrow S\left( x \right) = {6^2}\arccos \left( {1 - \frac{x}{{10}}} \right) - \frac{1}{2}.6.6.2\left( {1 - \frac{x}{{10}}} \right)\sqrt {1 - {{\left( {1 - \frac{x}{{10}}} \right)}^2}} \)
\( \Rightarrow V = \int\limits_0^{10} {S\left( x \right){\rm{d}}x} = \int\limits_0^{10} {\left( {36\arccos \left( {1 - \frac{x}{{10}}} \right) - 36\left( {1 - \frac{x}{{10}}} \right)\sqrt {1 - {{\left( {1 - \frac{x}{{10}}} \right)}^2}} } \right){\rm{d}}x} = 240\).
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn B
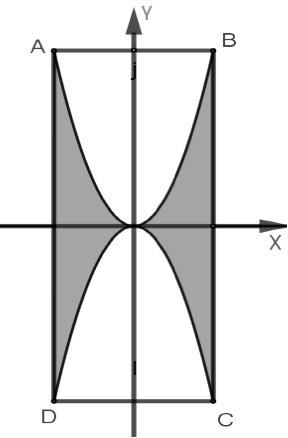
Vì \(AB = 4dm;BC = 8dm.\)\( \Rightarrow A( - 2;4),\)\(B(2;4),C(2; - 4),D( - 2; - 4)\).
parabol là: \(y = {x^2}\) hoặc \(y = - {x^2}\)
Diện tích phần tô đậm là \[{S_1} = 4\int\limits_0^2 {{x^2}dx = \frac{{32}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})} \]
Diện tích hình chữ nhật là \[S = 4.8 = 32\begin{array}{*{20}{c}}{}\end{array}({m^2})\]
Diện tích phần trắng là \[{S_2} = S - {S_1} = 32 - \frac{{32}}{3} = \frac{{64}}{3}\begin{array}{*{20}{c}}{}\end{array}(d{m^2})\]
Tổng chi phí trang chí là:
Lời giải
Chọn D
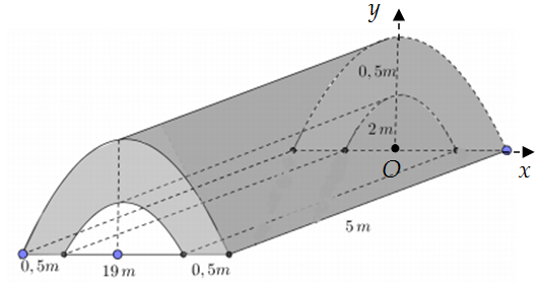
Chọn hệ trục \[Oxy\] như hình vẽ.
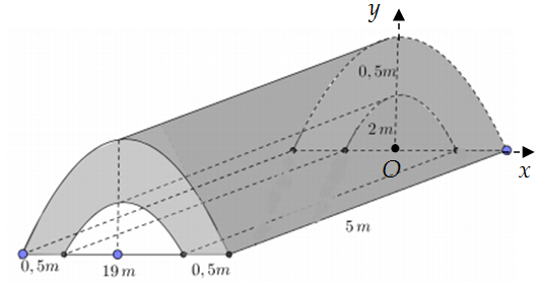
Gọi \[\left( {{P_1}} \right):y = {a_1}{x^2} + {b_1}\] là Parabol đi qua hai điểm \[A\left( {\frac{{19}}{2};0} \right),B\left( {0;2} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = a.{\left( {\frac{{19}}{2}} \right)^2} + 2\\2 = b\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_1} = - \frac{8}{{361}}\\{b_1} = 2\end{array} \right.\]\[ \Rightarrow \left( {{P_1}} \right):y = - \frac{8}{{361}}{x^2} + 2\].
Gọi \[\left( {{P_2}} \right):y = {a_2}{x^2} + {b_2}\] là Parabol đi qua hai điểm \[C\left( {10;0} \right),D\left( {0;\frac{5}{2}} \right)\]
Nên ta có hệ phương trình sau: \[\left\{ \begin{array}{l}0 = {a_2}.{\left( {10} \right)^2} + \frac{5}{2}\\\frac{5}{2} = {b_2}\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{a_2} = - \frac{1}{{40}}\\{b_2} = \frac{5}{2}\end{array} \right.\]\[ \Rightarrow \left( {{P_2}} \right):y = - \frac{1}{{40}}{x^2} + \frac{5}{2}\].
Ta có thể tích của bê tông là: \[V = 5.2\left[ {\int_0^{10} {\left( { - \frac{1}{{40}}{x^2} + \frac{5}{2}} \right)} {\rm{d}}x - \int_0^{\frac{{19}}{2}} {\left( { - \frac{8}{{361}}{x^2} + 2} \right)} {\rm{d}}x} \right] = 40\,{{\rm{m}}^3}\].
Số tiền mà tỉnh Phú Yên cần bỏ ra để xây cây cầu là: \[5.40 = 200\] triệu đồng
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho một mô hình [3D] mô phỏng một đường hầm như hình vẽ bên. Biết rằng đường hầm mô hình có chiều dài (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/07/blobid13-1753788326.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo