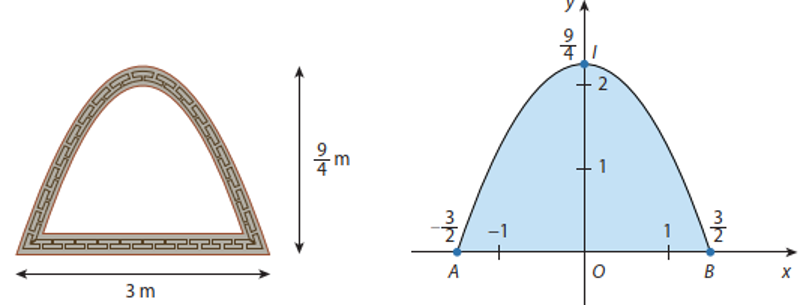
Cửa vòm lấy ánh sáng của một tòa nhà được thiết kế dạng parabol với kích thước như hình vẽ. Người ta định lắp kính cho cửa này. Tính diện tích kính cần lắp, biết rằng người ta chỉ sử dụng một lớp kính và bỏ qua diện tích của khung cửa.
Trả lời: ………………..
Cửa vòm lấy ánh sáng của một tòa nhà được thiết kế dạng parabol với kích thước như hình vẽ. Người ta định lắp kính cho cửa này. Tính diện tích kính cần lắp, biết rằng người ta chỉ sử dụng một lớp kính và bỏ qua diện tích của khung cửa.

Trả lời: ………………..
Quảng cáo
Trả lời:
Cửa có hình dạng một parabol \((P)\) với phương trình \(y = a{x^2} + bx + c\).
Parabol \((P)\) có đỉnh \(I\left( {0;\frac{9}{4}} \right)\) nên \(c = \frac{9}{4}\), suy ra \((P):y = a{x^2} + bx + \frac{9}{4}\).
Vì parabol \((P)\) đi qua các điểm \(A\left( { - \frac{3}{2},0} \right),B\left( {\frac{3}{2};0} \right)\) nên \(\left\{ {\begin{array}{*{20}{l}}{\frac{9}{4}a - \frac{3}{2}b = - \frac{9}{4}}\\{\frac{9}{4}a + \frac{3}{2}b = - \frac{9}{4}}\end{array}} \right.\), suy ra \(\left\{ {\begin{array}{*{20}{l}}{a = - 1}\\{b = 0}\end{array}} \right.\)
Do đó \((P):y = - {x^2} + \frac{9}{4}\).
Gọi \(S\left( {\;{{\rm{m}}^2}} \right)\) là diện tích kính cẩn lắp. Ta có \(S\) bằng diện tích hình phẳng \((H)\) giới hạn bởi parabol, trục hoành và các đường thẳng \(x = - \frac{3}{2},x = \frac{3}{2}\).
\(S = \int_{ - \frac{3}{2}}^{\frac{3}{2}} {\left( { - {x^2} + \frac{9}{4}} \right)} {\rm{d}}x = \left. {\left( { - \frac{{{x^3}}}{3} + \frac{9}{4}x} \right)} \right|_{ - \frac{3}{2}}^{\frac{3}{2}} = \frac{9}{2}\left( {{m^2}} \right)\)
Vậy diện tích kính cản lắp là \(\frac{9}{2}{m^2}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\frac{{128}}{7}\)
Diện tích thiết diện là \(S\left( x \right) = \sqrt {{x^3}} .\sqrt {{x^3}} = {x^6}\).
Thể tích của vật thể \(\left( T \right)\) là \(V = \int\limits_0^2 {S\left( x \right)} dx = \int\limits_0^2 {{x^6}} dx = \frac{{128}}{7}\).
Lời giải
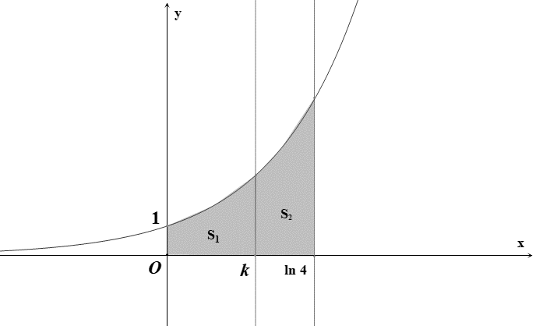
\[k = \ln 3\]
Diện tích hình thang cong \[\left( H \right)\] giới hạn bởi các đường \[y = {{\rm{e}}^x}\], \[y = 0\], \[x = 0\], \[x = \ln 4\] là
\[S = \int\limits_0^{\ln 4} {{{\rm{e}}^x}{\rm{d}}x} = \left. {{{\rm{e}}^x}} \right|_0^{\ln 4} = \]\[{{\rm{e}}^{\ln 4}} - {{\rm{e}}^0} = 4 - 1 = 3\](đvdt).
Ta có \[S = {S_1} + {S_2} = {S_1} + \frac{1}{2}{S_1} = \frac{3}{2}{S_1}\]. Suy ra \[{S_1} = \frac{{2S}}{3} = \frac{{2.3}}{3} = 2\] (đvdt).
Vì \[{S_1}\] là phần diện tích được giới hạn bởi các đường \[y = {{\rm{e}}^x}\], \[y = 0\], \[x = 0\], \[x = k\] nên
\[2 = {S_1} = \int\limits_0^k {{{\rm{e}}^x}{\rm{d}}x} = \left. {{{\rm{e}}^x}} \right|_0^k = \]\[{{\rm{e}}^k} - {{\rm{e}}^0} = {{\rm{e}}^k} - 1\].
Do đó \[{{\rm{e}}^k} = 3 \Leftrightarrow k = \ln 3\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.