Tam thức bậc hai \(f\left( x \right) = {x^2} - ax + b\) có bảng xét dấu như hình vẽ:
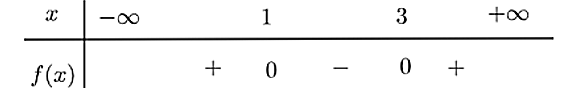
a) \(f\left( x \right) < 0 \Leftrightarrow 1 < x < 3\).
b) \(a + b = 7\).
c) \(f\left( 4 \right) = 3\).
d) Bảng xét dấu của đa thức \(g\left( x \right) = \left( {{x^2} - 3x + 2} \right)f\left( x \right)\) như sau:
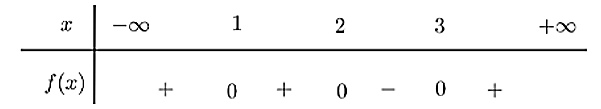
Quảng cáo
Trả lời:
Lời giải
a) Đúng. Quan sát bảng xét dấu, ta thấy \(f\left( x \right) < 0 \Leftrightarrow 1 < x < 3\).
b) Đúng. Nhận thấy \(f\left( x \right)\) có hai nghiệm \(x = 1\) và \(x = 3\).
Khi đó, ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = 0\\f\left( 3 \right) = 0\end{array} \right.\), tức là \(\left\{ \begin{array}{l}{1^2} - a \cdot 1 + b = 0\\{3^2} - a \cdot 3 + b = 0\end{array} \right.\). Ta tính được \(\left\{ \begin{array}{l}a = 4\\b = 3\end{array} \right.\).
Vậy \(a + b = 7\).
c) Đúng. Từ câu b) ta có \(f\left( x \right) = {x^2} - 4x + 3\). Khi đó, \(f\left( 4 \right) = {4^2} - 4 \cdot 4 + 3 = 3\).
d) Đúng. Ta có \(g\left( x \right) = \left( {{x^2} - 3x + 2} \right)f\left( x \right)\).
Tam thức bậc hai \(h\left( x \right) = {x^2} - 3x + 2\) có hai nghiệm \(x = 1\), \(x = 2\) và hệ số \(a = 1 > 0\).
Ta có bảng xét dấu như sau:
|
\(x\) |
\( - \infty \) \(1\) \(2\) \(3\) \( + \infty \) |
|
\(h\left( x \right)\) |
+ \(0\) \( - \) \(0\) + | + |
|
\(f\left( x \right)\) |
+ \(0\) \( - \) | \( - \) \(0\) + |
|
\(g\left( x \right) = h\left( x \right)f\left( x \right)\) |
+ \(0\) + \(0\) \( - \) \(0\) + |
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Xét hàm số bậc hai \(y = a{t^2} + bt + c\,\,\left( {a \ne 0} \right)\).
Theo giả thiết, ta có: \(\left\{ {\begin{array}{*{20}{l}}{c = 0}\\{ - \frac{b}{{2a}} = 3}\\{9a + 3b + c = 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{c = 0}\\{6a + b = 0}\\{9a + 3b = 21}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{7}{3}}\\\begin{array}{l}b = 14\\c = 0\end{array}\end{array}} \right.\).
Vì vậy \(y = - \frac{7}{3}{t^2} + 14t\).
Ta cần xét: \(y = - \frac{7}{3}{t^2} + 14t > 10\) hay \( - \frac{7}{3}{t^2} + 14t - 10 > 0\).
Đặt \(f\left( t \right) = - \frac{7}{3}{t^2} + 14t - 10;\) cho \(f\left( t \right) = 0 \Rightarrow {t_1} = \frac{{21 - \sqrt {231} }}{7},{t_2} = \frac{{21 + \sqrt {231} }}{7}\).
Bảng xét dấu \(f\left( t \right)\):

Kết luận: \(f\left( t \right) > 0\) khi \({t_1} < t < {t_2}\) hay \(\underbrace {\frac{{21 - \sqrt {231} }}{7}}_{ \approx 0,83} < t < \underbrace {\frac{{21 + \sqrt {231} }}{7}}_{ \approx 5,17}\).
Vì \(t\) nguyên nên \(t \in \left[ {1\,;5} \right]\). Do vậy giá trị \(t = 5\) thỏa mãn đề bài.
Đáp án: 5.
Lời giải
Lời giải
Ta có điều kiện: \( - 20 < x < 30\).
Diện tích hình chữ nhật lúc sau là: \(S = \left( {30 - x} \right) \cdot \left( {20 + x} \right) = - {x^2} + 10x + 600\;\,\,({\rm{c}}{{\rm{m}}^{\rm{2}}})\).
Diện tích hình chữ nhật lúc đầu là \(600\;\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Đặt \(f\left( x \right) = - {x^2} + 10x + 600 - 600 = - {x^2} + 10x\).
\(f\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 0}\\{x = 10}\end{array}} \right.\). Ta có bảng xét dấu của \(f\left( x \right)\):

Diện tích của khung sau khi uốn tăng lên khi \(f\left( x \right) > 0 \Leftrightarrow x \in \left( {0;\,10} \right)\).
Vậy \(a + b = 10\).
Đáp án: 10.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Một công ty Du lịch sinh thái thông báo giá tiền khi tham gia chuyến tham quan của một nhóm khách du lịch được cho như sau:
|
Số khách |
20 khách đầu tiên |
từ khách thứ 21 trở đi |
|
Giá tiền |
30 USD/người |
Giảm 1 USD/người cho toàn bộ khách trong nhóm |
Gọi x là số lượng khách từ người thứ 21 trở đi của nhóm.
a) Số khách tham quan chuyến du lịch trên là \(20 - x\).
b) Giá vé của mỗi người là \(30 - x\).
c) Doanh thu của công ty được tính bởi công thức \( - {x^2} + 10x + 600\).
d) Biết chi phí của chuyến tham quan mà công ty phải chịu là 400 USD. Khi đó, nếu số khách từ người thứ 21 trở lên của nhóm nhiều hơn 20 người thì công ty có lãi.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.