Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Ta có bảng thống kê sau:
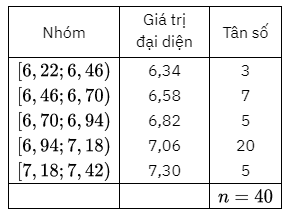
a) Số trung bình cộng của mẫu số liệu ghép nhóm là:
\({\bar x_D} = \frac{{3 \cdot 6,34 + 7 \cdot 6,58 + 5 \cdot 6,82 + 20 \cdot 7,06 + 5 \cdot 7,30}}{{40}} = \frac{{276,88}}{{40}} \approx 6,92(\;{\rm{m}})\)
Vậy phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng phần trăm):
\(\begin{array}{l}s_D^2 = \frac{1}{{40}}\left[ {3 \cdot {{(6,34 - 6,92)}^2} + 7 \cdot {{(6,58 - 6,92)}^2} + 5 \cdot {{(6,82 - 6,92)}^2}} \right.\left. { + 20 \cdot {{(7,06 - 6,92)}^2} + 5 \cdot {{(7,30 - 6,92)}^2}} \right]\\{\rm{ }} = \frac{{2,9824}}{{40}} \approx 0,07\end{array}\)Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: \({s_D} \approx \sqrt {0,07} \approx 0,26(\;{\rm{m}})\).
b) Ta có bảng thống kê sau:
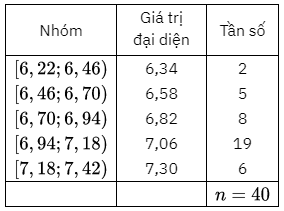
b) Số trung bình cộng của mẫu số liệu ghép nhóm là:
\({\bar x_H} = \frac{{2 \cdot 6,34 + 5 \cdot 6,58 + 8 \cdot 6,82 + 19 \cdot 7,06 + 6 \cdot 7,30}}{{40}} = \frac{{278,08}}{{40}} \approx 6,95(\;{\rm{m}})\)
Vậy phương sai của mẫu số liệu ghép nhóm (làm tròn kết quả đến hàng phẩn trăm):
\(\begin{array}{l}s_H^2 = \frac{1}{{40}}\left[ {2 \cdot {{(6,34 - 6,95)}^2} + 5 \cdot {{(6,58 - 6,95)}^2}} \right. + 8 \cdot {(6,82 - 6,95)^2} + 19 \cdot {(7,06 - 6,95)^2}\left. { + 6 \cdot {{(7,30 - 6,95)}^2}} \right]\\{\rm{ }} = \frac{{2,5288}}{{40}} \approx 0,06\end{array}\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: \({s_H} \approx \sqrt {0,06} \approx 0,24(\;{\rm{m}})\)
d)
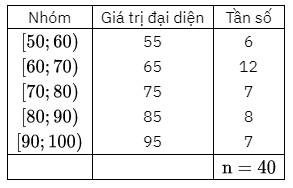
Số trung bình cộng của mẫu số liệu ghép nhóm trên là:
\(\bar x = \frac{{6.55 + 12 \cdot 65 + 7.75 + 8.85 + 7.95}}{{40}} = \frac{{2980}}{{40}} = 74,5.{\rm{ }}\)
Vậy phương sai của của mẫu số liệu ghép nhóm trên là:
\(\begin{array}{l}{s^2} = \frac{1}{{40}} \cdot \left[ {6 \cdot {{(55 - 74,5)}^2} + 12 \cdot {{(65 - 74,5)}^2} + 7 \cdot {{(75 - 74,5)}^2}} \right.\left. { + 8 \cdot {{(85 - 74,5)}^2} + 7 \cdot {{(95 - 74,5)}^2}} \right]\\{\rm{ }} = \frac{{7190}}{{40}} \approx 179,8\end{array}\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm trên là: \(s \approx \sqrt {179,8} \approx 13,4\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có bảng thống kê giá đóng cửa theo giá trị đại diện:
Xét mẫu số liệu của cổ phiếu A:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_1} = \frac{{8.121 + 9.123 + 12.125 + 10.127 + 11.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_1^2\] = \[\frac{1}{{50}}\] (8 . 1212 + 9 . 1232 + 12 . 1252 + 10 . 1272 + 11 . 1292) – (125,28)2 = 7,5216.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_1} = \sqrt {S_1^2} = \sqrt {7,5216} \]
Xét mẫu số liệu của cổ phiếu B:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_2} = \frac{{16.121 + 4.123 + 3.125 + 6.127 + 21.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_2^2\]=\[\frac{1}{{50}}\] (16 . 1212 + 4 . 1232 + 3 . 1252 + 6 . 1272 + 21 . 1292) – (125,48)2 = 12,4096.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} = \sqrt {S_2^2} = \sqrt {12,4096} \]
Vậy nếu đánh giá độ rủi ro theo phương sai và độ lệch chuẩn thì cổ phiếu A có độ rủi ro thấp hơn cổ phiếu B.
Lời giải
a) Cỡ mẫu là n = 20.
Số trung bình của mẫu số liệu trên là: \[{\bar x_1} = \frac{{111,6 + 134,9 + ... + 114}}{{20}} = 122,755\]
Phương sai của mẫu số liệu trên là: S12 =\[\frac{1}{{20}}\] (111,62 + 134,92 + … + 1142) – 122,7552 ≈ 515,453.
Độ lệch chuẩn của mẫu số liệu trên là \[{S_1} \approx \sqrt {515,453} \approx 22,704\]
b) Ta có bảng sau:
Số trung bình của mẫu số liệu ghép nhóm là: \[{\bar x_2} = \frac{{3.89 + 6.107 + 3.125 + 5.143 + 3.161}}{{20}} = 124,1\]
Phương sai của mẫu số liệu ghép nhóm là
S22 = \[\frac{1}{{20}}\] (3 . 892 + 6 . 1072 + 3 . 1252 + 5 . 1432 + 3 . 1612) – 124,12 = 566,19.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} \approx \sqrt {566,19} \approx 23,795\]
c) Sai số tương đối của độ lệch chuẩn của mẫu số liệu ghép nhóm so với độ lệch chuẩn của mẫu số liệu gốc là
\[\frac{{\left| {{S_2} - {S_1}} \right|}}{{{S_1}}} = \frac{{\left| {23,795 - 22,704} \right|}}{{22,704}} \cdot 100\% \approx 4,805\% \]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo