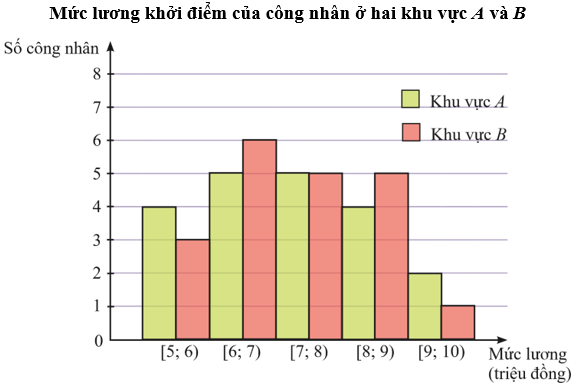
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau:
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả đo của An và Bình. Từ đó kết luận xem vôn kế của bạn nào cho kết quả đo ổn định hơn.
Trong bài thực hành đo hiệu điện thế của mạch điện, An và Bình đã dùng hai vôn kế khác nhau để đo, mỗi bạn tiến hành đo 10 lần cho kết quả như sau:
Tính độ lệch chuẩn của các mẫu số liệu ghép nhóm cho kết quả đo của An và Bình. Từ đó kết luận xem vôn kế của bạn nào cho kết quả đo ổn định hơn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn giá trị đại diện cho mẫu số liệu ta có:
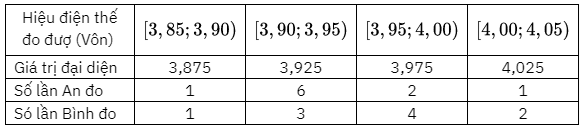
Hiệu điện thế trung bình của An đo là: \(\overline {{x_1}} = \frac{{3,875 \cdot 1 + 3,925 \cdot 6 + 3,975 \cdot 2 + 4,025.1}}{{10}} = 3,94.{\rm{ }}\)
Hiệu điện thế trung bình của Bình đo là: \(\overline {{x_2}} = \frac{{3,875.1 + 3,925.3 + 3,975.4 + 4,025.2}}{{10}} = 3,96\)
Phương sai và độ lệch chuẩn về mẫu số liệu ghép nhóm của An đo là:
\(s_1^2 = \frac{{{{3,875}^2} \cdot 1 + {{3,925}^2} \cdot 6 + {{3,975}^2} \cdot 2 + {{4,025}^2} \cdot 1}}{{10}} - {3,94^2} = 1,525 \cdot {10^{ - 3}}{\rm{. }}\)Suy ra \({s_1} = \sqrt {1,525 \cdot {{10}^{ - 3}}} \approx 0,039\).
Phương sai và độ lệch chuẩn về mẫu số liệu ghép nhóm của Bình đo là:
\(s_2^2 = \frac{{{{3,875}^2} \cdot 1 + {{3,925}^2} \cdot 3 + {{3,975}^2} \cdot 4 + {{4,025}^2} \cdot 2}}{{10}} - {3,96^2} = 2,025 \cdot {10^{ - 3}}{\rm{. }}\)Suy ra \({s_2} = \sqrt {2,025 \cdot {{10}^{ - 3}}} = 0,045\).
Dựa vào kết quả tính được của độ lệch chuẩn, ta thấy vôn kế của An cho kết quảồn định hơn vôn kế của Bình.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có bảng thống kê giá đóng cửa theo giá trị đại diện:
Xét mẫu số liệu của cổ phiếu A:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_1} = \frac{{8.121 + 9.123 + 12.125 + 10.127 + 11.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_1^2\] = \[\frac{1}{{50}}\] (8 . 1212 + 9 . 1232 + 12 . 1252 + 10 . 1272 + 11 . 1292) – (125,28)2 = 7,5216.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_1} = \sqrt {S_1^2} = \sqrt {7,5216} \]
Xét mẫu số liệu của cổ phiếu B:
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_2} = \frac{{16.121 + 4.123 + 3.125 + 6.127 + 21.129}}{{50}} = 125,28\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_2^2\]=\[\frac{1}{{50}}\] (16 . 1212 + 4 . 1232 + 3 . 1252 + 6 . 1272 + 21 . 1292) – (125,48)2 = 12,4096.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_2} = \sqrt {S_2^2} = \sqrt {12,4096} \]
Vậy nếu đánh giá độ rủi ro theo phương sai và độ lệch chuẩn thì cổ phiếu A có độ rủi ro thấp hơn cổ phiếu B.
Lời giải
a) Ta có bảng sau:
b) Xét mẫu số liệu của khu vực A: Cỡ mẫu là nA = 4 + 5 + 5 + 4 + 2 = 20.
Số trung bình của mẫu số liệu ghép nhóm là: \[{\bar x_A} = \frac{{4.5,5 + 5.6,5 + 5.7,5 + 4.8,5 + 2.9,5}}{{20}} = 7,25\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_A^2\]= \[\frac{1}{{20}}\] (4 . 5,52 + 5 . 6,52 + 5 . 7,52 + 4 . 8,52 + 2 . 9,52) – (7,25)2 = 1,5875.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_A} \approx \sqrt {1,5875} \]
Xét mẫu số liệu của khu vực B: Cỡ mẫu là nB = 3 + 6 + 5 + 5 + 1 = 20.
Số trung bình của mẫu số liệu ghép nhóm là \[{\bar x_B} = \frac{{3.5,5 + 6.6,5 + 5.7,5 + 5.8,5 + 1.9,5}}{{20}} = 7,25\]
Phương sai của mẫu số liệu ghép nhóm là
\[S_B^2\] = \[\frac{1}{{20}}\] (3 . 5,52 + 6 . 6,52 + 5 . 7,52 + 5 . 8,52 + 1 . 9,52) – (7,25)2 = 1,2875.
Độ lệch chuẩn của mẫu số liệu ghép nhóm là \[{S_B} \approx \sqrt {1,2875} \]
Do SA > SB nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực B đồng đều hơn của công nhân khu vực A.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo