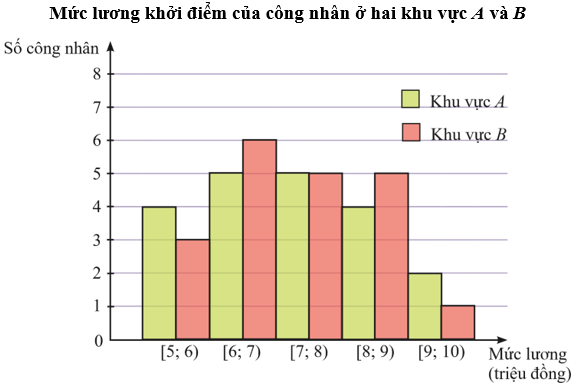
Điều tra thời gian phải làm thêm trung bình hằng tuần của các bác sĩ ở một bệnh viện, người ta thu được số liệu sau:

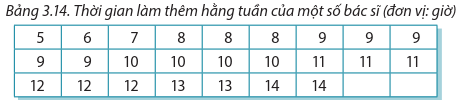
a)      Chuyển mẫu số liệu đã cho về mẫu số liệu ghép nhóm với độ dài các nhóm ghép bằng 2 và nhóm đầu tiên là [5; 7).

b)     Tính số trung bình, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm lập ở câu a (làm tròn kết quả đến hàng phần trăm).

c)      So sánh và nêu ý nghĩa các kết quả tìm được ở câu b với các kết quả tương ứng của mẫu số liệu gốc.

a) Căn cứ vào giá trị nhỏ nhất và giá trị lớn nhất của mẫu số liệu, ta thấy khoảng biến thiên là \(R = 9\) nên nếu muốn mỗi nhóm có độ dài bằng 2 và nhóm đầu tiên là \([5;7)\) thì phải chia số liệu thành 5 nhóm, với 4 nhóm ghép tiếp theo là \([7;9),[9;11),[11;13),[13;15)\). Đếm số lần xuất hiện các giá trị trong mỗi nhóm, ta lập được bảng sau:

Bảng 3.15a. Thời gian làm thêm hằng tuẩn của một số bác sí (đơn vị: giờ)

b) Bổ sung thêm giá trị đại diện của mỗi nhóm vào bảng lập ở trên, ta có Bảng 3.15b:

Sử dụng bảng 3.15b để tính số trung bình \({\bar x_N}\) của mẫu số liệu ghép nhóm:

\({\bar x_N} = \frac{{2.6 + 4.8 + 9.10 + 6.12 + 4.14}}{{25}} = \frac{{262}}{{25}} = 10,48{\rm{ (gio)}}{\rm{. }}\)

Suy ra phương sai \(s_N^2\) của mẫu số liệu ghép nhóm là:

\( = \frac{{2{{(6 - 10,48)}^2} + 4{{(8 - 10,48)}^2} + 9{{(10 - 10,48)}^2} + 6{{(12 - 10,48)}^2} + 4{{(14 - 10,48)}^2}}}{{25}} = \frac{{130,24}}{{25}} = 5,2096 \approx 5,21.\)Độ lệch chuẩn \({s_N}\) của mẫu số liệu ghép nhóm là \({s_N} = \sqrt {s_N^2}  \approx 2,28\).

c) Gọi \({\bar x_G},s_G^2,{s_G}\) tương ứng là trung bình, phương sai, độ lệch chuẩn của mẫu số liệu gốc. Để tính giá trị của các số đặc trưng này, ta lập bảng tần số:

Sử dụng các công thức tính trung bình, phương sai, độ lệch chuẩn của mẫu số liệu không ghép nhóm, ta có: \({\bar x_G} = \frac{{5 + 6 + 7 + 3.8 + 5.9 + 4.10 + 3.11 + 3.12 + 2.13 + 2.14}}{{25}} = 10.\)

Phương sai:

\(s_G^2 = \frac{{1{{(5 - 10)}^2} + 1{{(6 - 10)}^2} + 1{{(7 - 10)}^2} +  \ldots  + 3{{(12 - 10)}^2} + 2{{(13 - 10)}^2} + 2{{(14 - 10)}^2}}}{{25}} = \frac{{132}}{{25}} = 5,28.\)

Độ lệch chuẩn: \({s_G} = \sqrt {s_G^2}  = \sqrt {5,28}  \approx 2,30\).

Quan sát kết quả tìm được ở hai câu b và \(c\), ta thấy \({\bar x_N} \approx {\bar x_G};s_N^2 \approx s_G^2;{s_N} \approx {s_G}\). Như vậy số trung bình, phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm tương ứng xấp xỉ với số trung bình, phương sai, độ lệch chuẩn của mẫu số liệu ban đầu, khi chưa ghép nhóm. Nếu chỉ có mẫu số liệu ghép nhóm thì ta có thể kết luận là thời gian làm thêm trung bình hằng tuần của 25 bác sĩ được điều tra là 10,48 giờ và so với số này thì thời gian làm thêm của các bác sĩ chênh lệch trung bình khoảng 2,28 giờ.