Cho mặt phẳng \(\left( {{P_1}} \right):2x - 4y - 4z + 3 = 0\) và mặt phẳng \(\left( {{P_2}} \right):x - 2y - 2z + 1 = 0\).
a) Chứng minh rằng \(\left( {{P_1}} \right)//\left( {{P_2}} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(\left( {{P_1}} \right),\left( {{P_2}} \right)\).
Cho mặt phẳng \(\left( {{P_1}} \right):2x - 4y - 4z + 3 = 0\) và mặt phẳng \(\left( {{P_2}} \right):x - 2y - 2z + 1 = 0\).
a) Chứng minh rằng \(\left( {{P_1}} \right)//\left( {{P_2}} \right)\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(\left( {{P_1}} \right),\left( {{P_2}} \right)\).
Quảng cáo
Trả lời:
a) Ta có \({\vec n_1} = (2; - 4; - 4),{\vec n_2} = (1; - 2; - 2)\) lần lượt là hai vectơ pháp tuyến của các mặt phẳng \(\left( {{P_1}} \right),\left( {{P_2}} \right)\). Do \({\vec n_1} = 2{\vec n_2},{D_1} = 3 \ne 2 = 2{D_2}\) nên \(\left( {{P_1}} \right)//\left( {{P_2}} \right)\).
b) Chọn điểm \({M_0}\left( { - \frac{3}{2};0;0} \right) \in \left( {{P_1}} \right)\). Suy ra khoảng cách từ điểm \({M_0}\) đến mặt phẳng \(\left( {{P_2}} \right)\) là:
\(d\left( {{M_0},\left( {{P_2}} \right)} \right) = \frac{{\left| { - \frac{3}{2} + 1} \right|}}{{\sqrt {{1^2} + {{( - 2)}^2} + {{( - 2)}^2}} }} = \frac{1}{6}.\)Nên khoảng cách giữa hai mặt phẳng song song \(\left( {{P_1}} \right),\left( {{P_2}} \right)\) bằng \(\frac{1}{6}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Mặt phẳng \((ABC)\) đi qua ba điểm \(A(1;1;1),B(2;3;4),C(5;2;3)\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} = (1;2;3),\overrightarrow {AC} = (4;1;2)\), suy ra \((ABC)\) có vectơ pháp tuyến \(\vec n = (2.2 - 3.1;3.4 - 1.2;1.1 - 2.4) = (1;10; - 7)\).
Phương trình của \((ABC)\) là: \(1(x - 1) + 10(y - 1) - 7(z - 1) = 0\) hay \(x + 10y - 7z - 4 = 0\).
Chiều cao SH cùa hình chóp S.ABC chính là khoàng cách từ điểm \(S\) đến \((ABC)\).
Ta có: \(SH = d(S,(ABC)) = \frac{{|1.5 + 10 \cdot 0 + ( - 7) \cdot 1 - 4|}}{{\sqrt {{1^2} + {{10}^2} + {{( - 7)}^2}} }} = \frac{6}{{5\sqrt 6 }} = \frac{{\sqrt 6 }}{5}\).
Lời giải
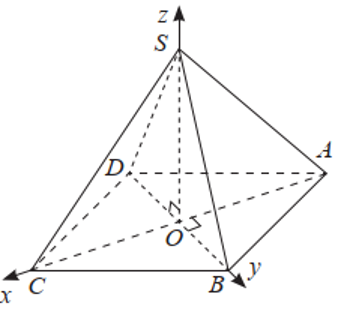
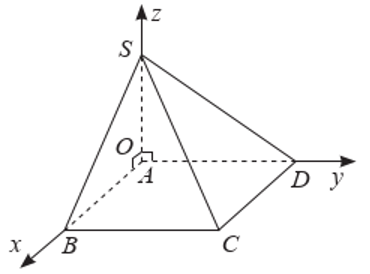
Dựa vào hệ trục toạ độ như hình vẽ, ta có \(O(0;0;0),S(0;0;2a)\), \(A( - a;0;0),B(0;a;0)\) và \(C(a;0;0)\).
Khi đó \((SAB)\) có phương trình là \(\frac{x}{{ - a}} + \frac{y}{a} + \frac{z}{{2a}} = 1\) hay \( - 2x + 2y + z - 2a = 0\).
Vậy \(d(C,(SAB)) = \frac{{| - 2 \cdot a - 2a|}}{{\sqrt {{{( - 2)}^2} + {2^2} + {1^2}} }} = \frac{{4a}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.