Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) : \(2x + 3y - 6z - 7 = 0,(\beta ):2x + 3y - 6z + 14 = 0\).
a) Tính khoảng cách từ gốc toạ độ và từ điểm \(M(1; - 2;3)\) đến \((\alpha )\).
b) Chứng minh \((\alpha )//(\beta )\) và tính khoảng cách giữa hai mặt phẳng \((\alpha )\) và \((\beta )\).
Trong không gian Oxyz, cho mặt phẳng \((\alpha )\) : \(2x + 3y - 6z - 7 = 0,(\beta ):2x + 3y - 6z + 14 = 0\).
a) Tính khoảng cách từ gốc toạ độ và từ điểm \(M(1; - 2;3)\) đến \((\alpha )\).
b) Chứng minh \((\alpha )//(\beta )\) và tính khoảng cách giữa hai mặt phẳng \((\alpha )\) và \((\beta )\).
Quảng cáo
Trả lời:
a) Áp dụng công thức tính khoảng cách, ta có:
\(\begin{array}{l}d(O,(\alpha )) = \frac{{|2.0 + 3.0 - 6.0 - 7|}}{{\sqrt {{2^2} + {3^2} + {{( - 6)}^2}} }} = \frac{7}{7} = 1\\d(M,(\alpha )) = \frac{{|2.1 + 3.( - 2) - 6.3 - 7|}}{{\sqrt {{2^2} + {3^2} + {{( - 6)}^2}} }} = \frac{{29}}{7}.\end{array}\)
b) Ta có \(\frac{2}{2} = \frac{3}{3} = \frac{{ - 6}}{{ - 6}} \ne \frac{{ - 7}}{{14}}\) nên \((\alpha )//(\beta )\). Lấy điểm \(N( - 7;0;0)\) thuộc ( \(\beta \) ).
Vậy \(d((\alpha ),(\beta )) = d(N,(\alpha )) = \frac{{|2.( - 7) + 3.0 - 6.0 - 7|}}{{\sqrt {{2^2} + {3^2} + {{( - 6)}^2}} }} = \frac{{21}}{7} = 3.{\rm{ }}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Mặt phẳng \((ABC)\) đi qua ba điểm \(A(1;1;1),B(2;3;4),C(5;2;3)\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} = (1;2;3),\overrightarrow {AC} = (4;1;2)\), suy ra \((ABC)\) có vectơ pháp tuyến \(\vec n = (2.2 - 3.1;3.4 - 1.2;1.1 - 2.4) = (1;10; - 7)\).
Phương trình của \((ABC)\) là: \(1(x - 1) + 10(y - 1) - 7(z - 1) = 0\) hay \(x + 10y - 7z - 4 = 0\).
Chiều cao SH cùa hình chóp S.ABC chính là khoàng cách từ điểm \(S\) đến \((ABC)\).
Ta có: \(SH = d(S,(ABC)) = \frac{{|1.5 + 10 \cdot 0 + ( - 7) \cdot 1 - 4|}}{{\sqrt {{1^2} + {{10}^2} + {{( - 7)}^2}} }} = \frac{6}{{5\sqrt 6 }} = \frac{{\sqrt 6 }}{5}\).
Lời giải
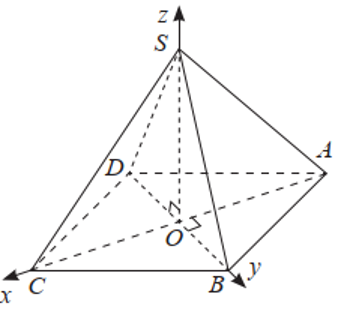
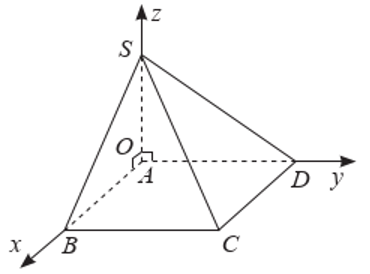
Dựa vào hệ trục toạ độ như hình vẽ, ta có \(O(0;0;0),S(0;0;2a)\), \(A( - a;0;0),B(0;a;0)\) và \(C(a;0;0)\).
Khi đó \((SAB)\) có phương trình là \(\frac{x}{{ - a}} + \frac{y}{a} + \frac{z}{{2a}} = 1\) hay \( - 2x + 2y + z - 2a = 0\).
Vậy \(d(C,(SAB)) = \frac{{| - 2 \cdot a - 2a|}}{{\sqrt {{{( - 2)}^2} + {2^2} + {1^2}} }} = \frac{{4a}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.