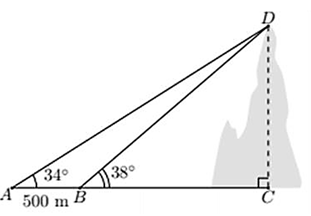
Tại hai điểm \[A,\,\,B\] cách nhau \[500{\rm{ m}},\] người ta nhìn thấy đỉnh núi với góc nâng lần lượt là \[34^\circ \] và \[38^\circ .\] Tính chiều cao của ngọn núi. (đơn vị: m; kết quả làm tròn đến hàng đơn vị)
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 9 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: 2468
Đặt \[BC = \;x\,\,({\rm{m}});\,\,AC = \;AB + \;BC = \;500 + \;x\,\,({\rm{m}}).\]
Xét tam giác \[ACD\] vuông tại \[C,\] ta có: \(\tan \widehat {CAD} = \frac{{CD}}{{AC}}.\)
Suy ra \[CD\; = \;AC \cdot \tan \widehat {CAD}\; = \;\left( {500\; + \;x} \right) \cdot \tan 34^\circ .\]
Xét tam giác \[BCD\] vuông tại \[C,\] ta có: \(\tan \widehat {CBD} = \frac{{CD}}{{BC}}.\)
Suy ra \[CD = BC \cdot \tan \widehat {CBD} = x \cdot \tan 38^\circ .\]
Do đó, ta có: \[\left( {500 + \;x} \right)\tan 34^\circ \; = \;x \cdot \tan 38^\circ \]
\[500 \cdot \tan 34^\circ \; + \,x \cdot \tan 34^\circ = \;x \cdot \tan 38^\circ \]
\[\;x \cdot \tan 38^\circ - x \cdot \tan 34^\circ = 500 \cdot \tan 34^\circ \]
\[\;x \cdot \left( {\tan 38^\circ - \tan 34^\circ } \right) = 500 \cdot \tan 34^\circ \]
\[\;x = \frac{{500 \cdot \tan 34^\circ }}{{\tan 38^\circ - \tan 34^\circ }}\].
Suy ra \[\;CD = \frac{{500 \cdot \tan 34^\circ }}{{\tan 38^\circ - \tan 34^\circ }} \cdot \tan 38^\circ \approx 2468\,\,({\rm{m}}).\]
Vậy ngọn núi cao khoảng \[2468\,\,{\rm{m}}{\rm{.}}\]
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 120.
Đổi 20 phút \( = \frac{1}{3}\) giờ.
Gọi quãng đường \[AB\] là \[x\,\,\left( {{\rm{km}}} \right)\,\,\left( {x > 0} \right).\]
Thời gian đi từ A đến B là \(\frac{x}{{40}}\) (giờ).
Lúc về người đó tăng vận tốc thêm 5 km/h nên vận tốc lúc về của người đó là \[40 + 5 = 45\,\,\left( {{\rm{km/h}}} \right).\]
Thời gian đi từ B về A là \(\frac{x}{{45}}\) (giờ).
Vì thời gian lúc về ít hơn thời gian lúc đi là 20 phút (\( = \frac{1}{3}\) giờ) nên ta có phương trình:
\(\frac{x}{{40}} - \frac{x}{{45}} = \frac{1}{3}\)
\(\frac{{9x}}{{360}} - \frac{{8x}}{{360}} = \frac{1}{3}\)
\(9x - 8x = 120\)
\(x = 120\) (TMĐK).
Vậy quãng đường AB là 120 km.
Lời giải
Đáp án: a) Đúng. b) Sai. c) Sai. d) Đúng.
a) Xét \[ABC\] cân tại \[A\] có \[AM\] là đường trung tuyến nên đồng thời là đường phân giác và đường cao của tam giác.
Xét \[\Delta ABM\] vuông tại \[M,\] khi đó \[\widehat {BAM}\] và B là hai góc phụ nhau, nên sin BAM cos B cos . Do đó ý a) Đúng.
b) và c)
Xét \[\Delta ABM\] vuông tại \[M,\] ta có: \(\cos B = \frac{{BM}}{{AB}}\,;\,\,\sin B = \frac{{AM}}{{AB}}.\)
Suy ra \[BM = AB \cdot \cos B = 2a \cdot \cos a\] và \[AM = \;AB \cdot \sin B = \;2a \cdot \sin \alpha .\]
Do đó ý b) và c) đều Sai.
d) Ta có \[BC = 2BM = 2 \cdot 2a \cdot \cos \alpha = 4a \cdot \cos \alpha .\]
Diện tích tam giác \[ABC\] là: \[S = \frac{1}{2} \cdot AM \cdot BC = \frac{1}{2} \cdot \left( {2a \cdot \sin \alpha } \right) \cdot \left( {4a \cdot \cos \alpha } \right) = 4{a^2} \cdot \sin \alpha \cdot \cos \alpha .\]
Do đó ý d) Đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo