Trong không gian với hệ trục tọa độ \[Oxyz\], cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\) và hình nón \(\left( H \right)\) có đỉnh \(A\left( {3;2; - 2} \right)\) và nhận \(AI\) làm trục đối xứng với \(I\) là tâm mặt cầu. Một đường sinh của hình nón \(\left( H \right)\) cắt mặt cầu tại \(M,{\rm{ }}N\) sao cho \(AM = 3AN\). Viết phương trình mặt cầu đồng tâm với mặt cầu \(\left( S \right)\) và tiếp xúc với các đường sinh của hình nón \(\left( H \right)\).

Xem lời giải

Câu hỏi trong đề: (Trả lời ngắn) 17 bài tập Phương trình mặt cầu (có lời giải) !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{71}}{3}\)

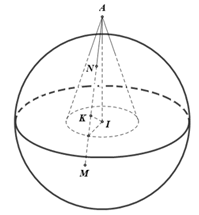
(Trả lời ngắn) Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu S: (x-1)^2 + (y-2)^2 + (z-3)^2 = 25 và hình nón H có đỉnh A(3; 2; -2) và nhận AI làm trục đối xứng với I là tâm mặt cầu (ảnh 1)

Gọi hình chiếu vuông góc của \(I\) trên \(MN\) là \(K\).

Dễ thấy \(AN = NK = \frac{1}{3}AM\), mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = 5\)

Có \(AM.AN = A{I^2} - {R^2} = 4 \Rightarrow A{N^2} = \frac{4}{3} \Rightarrow KN = AN = \frac{{2\sqrt 3 }}{3} \Rightarrow IK = \sqrt {I{N^2} - K{N^2}} = \frac{{\sqrt {213} }}{3}\).

Nhận thấy mặt cầu đồng tâm với mặt cầu \(\left( S \right)\) và tiếp xúc với các đường sinh của hình nón \(\left( H \right)\) chính là mặt cầu tâm \(I\left( {1;2;3} \right)\) có bán kính \(IK = \frac{{\sqrt {213} }}{3}\).

Vậy phương trình mặt cầu cần tìm là: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = \frac{{71}}{3}\).

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là kilômét) một trạm phát sóng điện thoại của nhà mạng Vinaphone được đặt ở vị trí \(I\left( {1; - 2; - 3} \right)\) và được thiết kế bán kính phủ sóng là \(5000m\).

a) Sử dụng phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng trong không gian.

b) Nhà bạn Minh Hiền và bạn Trúc Linh có vị trí tọa độ lần lượt là \(M\left( {1;2;0} \right)\) và \(N\left( { - 3;1;0} \right)\). Hỏi Minh Hiền và Trúc Linh dùng điện thoại tại nhà thì có thể sử dụng dịch vụ của trạm này không?

Xem đáp án

Lời giải

a) Phương trình mặt cầu để mô tả ranh giới bên ngoài vùng phủ sóng trong không gian là:

\({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 3} \right)^2} = 25\)

· Ta có: \(IM = \sqrt {{{\left( {1 - 1} \right)}^2} + {{\left( {2 + 2} \right)}^2} + {{\left( {0 + 3} \right)}^2}} = 5\)

Vì \(IM = R = 5\) nên điểm \(M\left( {1;2;0} \right)\) nằm trên mặt cầu . Vậy bạn Minh Hiền có thể sử dụng dịch vụ của trạm này.

· Ta có: \(IN = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {1 + 2} \right)}^2} + {{\left( {0 - 3} \right)}^2}} = \sqrt {34} > 5\)

Vì \(IN > R\) nên điểm \(N\left( { - 3;1;0} \right)\) nằm ngoài mặt cầu . Vậy bạn Trúc Linh không thể sử dụng dịch vụ của trạm này.

Câu 2

Trong không gian \(Oxyz\), tìm giá trị dương của \(m\) sao cho mặt phẳng \(\left( {Oxy} \right)\) tiếp xúc với mặt cầu \({\left( {x - 3} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = {m^2} + 1\).

Xem đáp án

Lời giải

Đáp án: \(m = \sqrt 3 \)

Mặt cầu \(\left( S \right)\): \({\left( {x - 3} \right)^2} + {y^2} + {\left( {z - 2} \right)^2} = {m^2} + 1\) có tâm \(I\left( {3\,;\,0\,;\,2} \right)\), bán kính \(R = \sqrt {{m^2} + 1} \).

\(\left( S \right)\) tiếp xúc với \(\left( {Oxy} \right)\)\( \Leftrightarrow d\left( {I,\left( {Oxy} \right)} \right) = R\)

\( \Leftrightarrow 2 = \sqrt {{m^2} + 1} \)\( \Leftrightarrow {m^2} = 3\)\( \Leftrightarrow m = \sqrt 3 \) (do \(m\) dương).

Câu 3