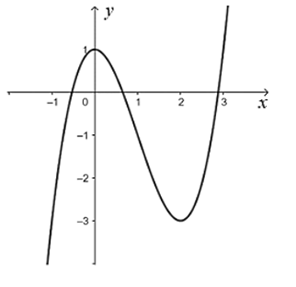
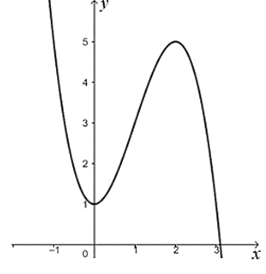
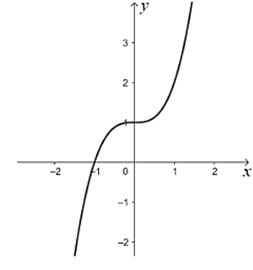
Cho hàm số \[y = f\left( x \right)\] liên tục và có bảng biến thiên trên đoạn \(\left[ { - 1;\,3} \right]\) như hình dưới đây.

Gọi \(M\) là giá trị lớn nhất của hàm số \[y = f\left( x \right)\] trên đoạn \[\left[ { - 1;\,\,3} \right]\]. Mệnh đề nào trong các mệnh đề sau đây là đúng?

Lời giải

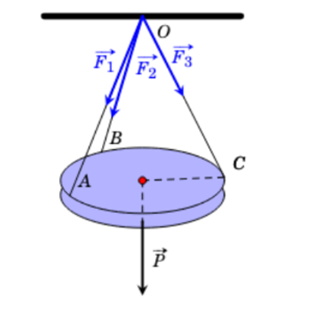
Ta có \(\overrightarrow {AD}  = \overrightarrow {BC} \) và \(\left( {\overrightarrow {AS} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AS} ,\overrightarrow {AD} } \right) = \widehat {SAD} = 60^\circ \).

Do đó \(\overrightarrow {AS}  \cdot \overrightarrow {BC}  = \overrightarrow {AS}  \cdot \overrightarrow {AD}  = \left| {\overrightarrow {AS} } \right| \cdot \left| {\overrightarrow {AD} } \right| \cdot \cos \widehat {SAD} = AS \cdot AD \cdot \cos 60^\circ  = 2 \cdot 2 \cdot \frac{1}{2} = 2\).

Đáp án: 2.

Lời giải

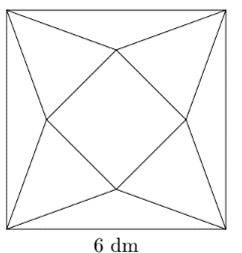
Giả sử miếng bìa hình vuông \(ABCD\), đáy của hình chóp tứ giác đều là hình vuông \(MNPQ\) tâm \(O\) có cạnh bằng \(x\) dm \(\left( {0 < x < 6\sqrt 2 } \right)\) như hình vẽ. Gọi \(H,\,K\) lần lượt là trung điểm của \(MQ\) và \(NP\).

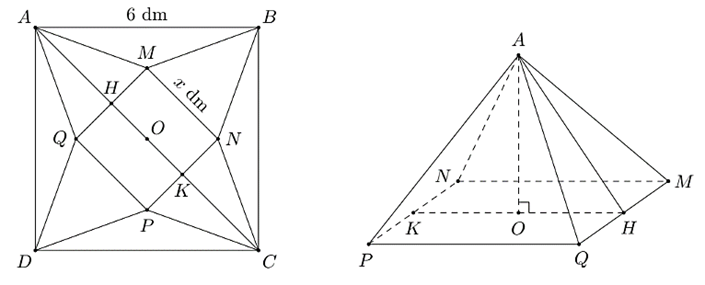
Vì \(ABCD\) là hình vuông cạnh bằng 6 dm nên \(AC = 6\sqrt 2 \) dm, \(HK = x\) dm.

Ta có \(AH = \frac{{AC - HK}}{2} = 3\sqrt 2  - \frac{x}{2}\) dm.

Đường cao của hình chóp tứ giác đều là:

\(h = AO = \sqrt {A{H^2} - O{H^2}}  = \sqrt {{{\left( {3\sqrt 2  - \frac{x}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}}  = \sqrt {18 - 3\sqrt 2 x} \) (dm).

Thể tích của khối chóp là: \(V = \frac{1}{3}h{x^2} = \frac{1}{3}{x^2}\sqrt {18 - 3\sqrt 2 x}  = \frac{1}{3}\sqrt {{x^4}\left( {18 - 3\sqrt 2 x} \right)} \) (dm3).

Để tìm giá trị lớn nhất của \(V\) ta đi tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^4}\left( {18 - 3\sqrt 2 x} \right)\) với \(0 < x \le 3\sqrt 2 \).

Ta có: \(f'\left( x \right) = {x^3}\left( { - 15\sqrt 2 x + 72} \right)\), \(f'\left( x \right) = 0\) khi \(x = 0\) hoặc \(x = \frac{{12\sqrt 2 }}{5}\).

Bảng biến thiên của hàm số \(f\left( x \right)\) như sau:

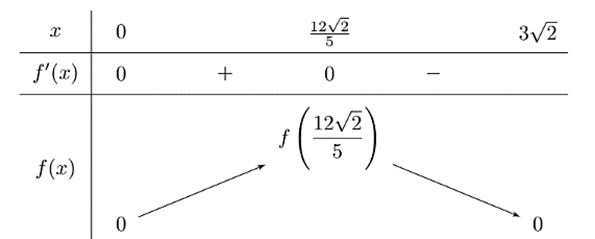
Từ bảng biến thiên, ta có \(\mathop {\max }\limits_{\left( {0;3\sqrt 2 } \right]} f\left( x \right) = f\left( {\frac{{12\sqrt 2 }}{5}} \right) = \frac{{1\,492\,992}}{{3125}}\).

Vậy thể tích của khối chóp có giá trị lớn nhất bằng \({V_{\max }} = \frac{1}{3}\sqrt {\frac{{1\,492\,992}}{{3125}}}  = \frac{{288\sqrt {10} }}{{125}}\) (dm3).