Dân số của một quốc gia sau \[t\] năm, kể từ năm \[2023\] được ước tính bởi công thức: \[N\left( t \right) = 100{e^{0,012t}}\]    \[\left( {N\left( t \right)} \right.\]được tính bằng triệu người, \[\left. {0 < t \le 50} \right).\] Biết rằng đạo hàm của hàm số \[N\left( t \right)\] biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm).

a) Ước tính dân số của quốc gia đó vào năm 2045 (đơn vị triệu người, kết quả làm tròn đến chữ số thập phân thứ hai).

b) Hỏi sau ít nhất bao nhiêu năm thì tốc độ tăng dân số của quốc gia đó sẽ lớn hơn \[1,8\] triệu người/năm?

Lời giải

Ta có \(\overrightarrow {AD}  = \overrightarrow {BC} \) và \(\left( {\overrightarrow {AS} ,\overrightarrow {BC} } \right) = \left( {\overrightarrow {AS} ,\overrightarrow {AD} } \right) = \widehat {SAD} = 60^\circ \).

Do đó \(\overrightarrow {AS}  \cdot \overrightarrow {BC}  = \overrightarrow {AS}  \cdot \overrightarrow {AD}  = \left| {\overrightarrow {AS} } \right| \cdot \left| {\overrightarrow {AD} } \right| \cdot \cos \widehat {SAD} = AS \cdot AD \cdot \cos 60^\circ  = 2 \cdot 2 \cdot \frac{1}{2} = 2\).

Đáp án: 2.

Lời giải

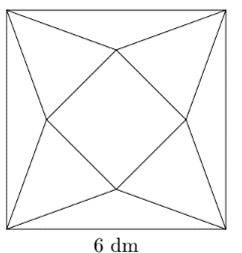
Giả sử miếng bìa hình vuông \(ABCD\), đáy của hình chóp tứ giác đều là hình vuông \(MNPQ\) tâm \(O\) có cạnh bằng \(x\) dm \(\left( {0 < x < 6\sqrt 2 } \right)\) như hình vẽ. Gọi \(H,\,K\) lần lượt là trung điểm của \(MQ\) và \(NP\).

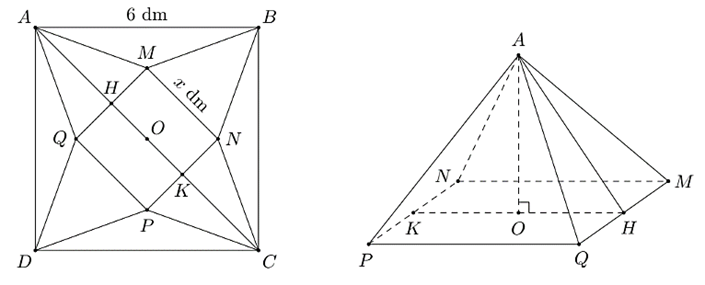
Vì \(ABCD\) là hình vuông cạnh bằng 6 dm nên \(AC = 6\sqrt 2 \) dm, \(HK = x\) dm.

Ta có \(AH = \frac{{AC - HK}}{2} = 3\sqrt 2  - \frac{x}{2}\) dm.

Đường cao của hình chóp tứ giác đều là:

\(h = AO = \sqrt {A{H^2} - O{H^2}}  = \sqrt {{{\left( {3\sqrt 2  - \frac{x}{2}} \right)}^2} - {{\left( {\frac{x}{2}} \right)}^2}}  = \sqrt {18 - 3\sqrt 2 x} \) (dm).

Thể tích của khối chóp là: \(V = \frac{1}{3}h{x^2} = \frac{1}{3}{x^2}\sqrt {18 - 3\sqrt 2 x}  = \frac{1}{3}\sqrt {{x^4}\left( {18 - 3\sqrt 2 x} \right)} \) (dm3).

Để tìm giá trị lớn nhất của \(V\) ta đi tìm giá trị lớn nhất của hàm số \(f\left( x \right) = {x^4}\left( {18 - 3\sqrt 2 x} \right)\) với \(0 < x \le 3\sqrt 2 \).

Ta có: \(f'\left( x \right) = {x^3}\left( { - 15\sqrt 2 x + 72} \right)\), \(f'\left( x \right) = 0\) khi \(x = 0\) hoặc \(x = \frac{{12\sqrt 2 }}{5}\).

Bảng biến thiên của hàm số \(f\left( x \right)\) như sau:

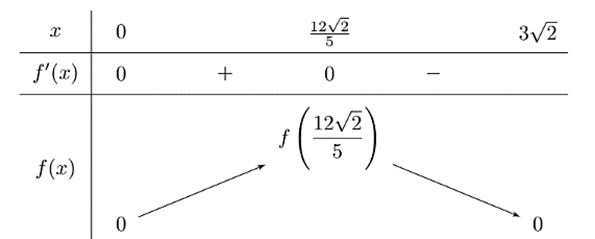
Từ bảng biến thiên, ta có \(\mathop {\max }\limits_{\left( {0;3\sqrt 2 } \right]} f\left( x \right) = f\left( {\frac{{12\sqrt 2 }}{5}} \right) = \frac{{1\,492\,992}}{{3125}}\).

Vậy thể tích của khối chóp có giá trị lớn nhất bằng \({V_{\max }} = \frac{1}{3}\sqrt {\frac{{1\,492\,992}}{{3125}}}  = \frac{{288\sqrt {10} }}{{125}}\) (dm3).