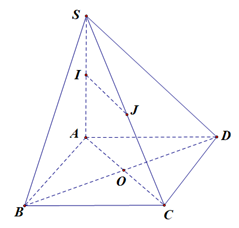
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\]là hình vuông, \(SA\)vuông góc với mặt phẳng \((ABCD)\).Gọi \[I,J\] lần lượt là trung điểm của \[SA,SC\]. \[G\]là trọng tâm tam giác \[SBD\]

a) \(\overrightarrow {AC}  - \overrightarrow {AB}  = \overrightarrow {AD} \).

b) \(\overrightarrow {AS}  + \overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AG} \).

c) \[\overrightarrow {{\rm{IJ}}} .\overrightarrow {BD}  = \overrightarrow 0 \]

d) \({\overrightarrow {AG} ^2} = {\overrightarrow {AS} ^2} + {\overrightarrow {AB} ^2} + {\overrightarrow {AD} ^2}\).

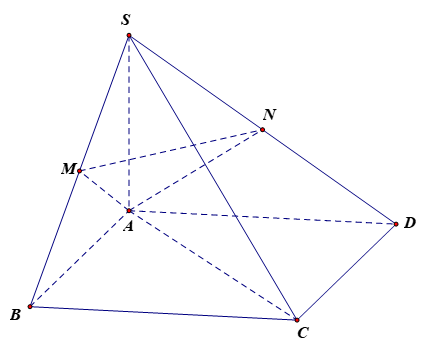
a) Vì ABCD là hình chữ nhật nên AB // CD nên hai vectơ \(\overrightarrow {AB} ,\overrightarrow {CD} \) là hai vectơ cùng phương, ngược hướng.

b) Ta có ABCD là hình chữ nhật nên \(AC = \sqrt {A{B^2} + A{D^2}} = a\sqrt 5 \).

Hình chóp S.ABCD có SA vuông góc với mặt đáy nên tam giác SAC là tam giác vuông tại A.

Suy ra \(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{2a}}{{a\sqrt 5 }} \Rightarrow \widehat {SCA} \approx 41^\circ 48'\).

Ta có \(\left( {\overrightarrow {SC} ,\overrightarrow {AC} } \right) = \left( {\overrightarrow {CS} ,\overrightarrow {CA} } \right) = \widehat {SCA} \approx 41^\circ 48'\).

c) Hình chóp S.ABCD có SA vuông góc với mặt đáy nên tam giác SAB là tam giác vuông tại A.

Suy ra \(SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 5 \).

Trong tam giác SAB vuông tại A có AM là đường trung tuyến nên \(AM = \frac{1}{2}SB = \frac{{a\sqrt 5 }}{2}\).

Lại có M là trung điểm của SB nên \(MB = \frac{1}{2}SB = \frac{{a\sqrt 5 }}{2}\).

Ta có \(\left( {\overrightarrow {AM} ,\overrightarrow {AB} } \right) = \widehat {MAB}\).

Xét MAB có \(\cos \widehat {MAB} = \frac{{M{A^2} + A{B^2} - M{B^2}}}{{2MA.AB}} = \frac{{\sqrt 5 }}{5}\).

Khi đó \(\overrightarrow {AM} .\overrightarrow {AB} = \left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AM} ,\overrightarrow {AB} } \right) = \frac{{a\sqrt 5 }}{2}.a.\frac{{\sqrt 5 }}{5} = \frac{{{a^2}}}{2}\).

d) Ta có M, N lần lượt là trung điểm của các cạnh SB, SD nên MN là đường trung bình của SBD.

Do đó \(MN = \frac{1}{2}BD = \frac{1}{2}\sqrt {A{B^2} + A{D^2}} = \frac{{a\sqrt 5 }}{2}\).

Suy ra \(\left| {\overrightarrow {AM} - \overrightarrow {AN} } \right| = \left| {\overrightarrow {MN} } \right| = \frac{{a\sqrt 5 }}{2}\).

Đáp án: a) Sai; b) Sai; c) Đúng; d) Sai.

Ta có \(\left( {\overrightarrow {SC} ,\overrightarrow {CA} } \right) = 180^\circ - 45^\circ = 135^\circ \); \(AC = \sqrt {{3^2} + {1^2}} = \sqrt {10} \).

Tam giác SAC vuông tại A, có \(SC = \frac{{AC}}{{\cos 45^\circ }} = \frac{{\sqrt {10} }}{{\frac{{\sqrt 2 }}{2}}} = 2\sqrt 5 \).

Ta có \(\overrightarrow {SC} .\overrightarrow {CA} = \left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {CA} } \right|.\cos \left( {\overrightarrow {SC} ,\overrightarrow {CA} } \right) = 2\sqrt 5 .\sqrt {10} .\cos 135^\circ = 2\sqrt 5 .\sqrt {10} .\left( {\frac{{ - \sqrt 2 }}{2}} \right) = - 10\).

Trả lời: −10.