Cho lăng trụ tam giác đều ABC.A'B'C' có AB = a và \(AA' = a\sqrt 2 \). Khi đó:

(a) \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \).

(b) Gọi M là trung điểm BC. Khi đó \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} \).

(c)\(\overrightarrow {A'M} .\overrightarrow {AC} = \frac{{{a^2}\sqrt 3 }}{4}\).

(d) Góc giữa vectơ \(\overrightarrow {AB'} \) và \(\overrightarrow {BC'} \) bằng 60°.

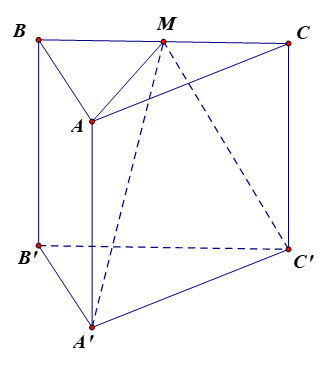
a) Ta có \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).

b) Ta có \(\overrightarrow {A'M} = \overrightarrow {A'A} + \overrightarrow {AM} \)\( = \overrightarrow {A'A} + \overrightarrow {AB} + \overrightarrow {BM} \)\( = \overrightarrow {A'A} + \overrightarrow {A'B'} + \overrightarrow {MC} \)\( = \overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} \).

c) \(\overrightarrow {A'M} .\overrightarrow {AC} = \left( {\overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} } \right).\overrightarrow {AC} \)\( = \overrightarrow {A'A} .\overrightarrow {AC} + \overrightarrow {A'B'} .\overrightarrow {AC} - \overrightarrow {CM} .\overrightarrow {AC} \)

\( = - \overrightarrow {AA'} .\overrightarrow {AC} + \overrightarrow {AB} .\overrightarrow {AC} + \overrightarrow {CM} .\overrightarrow {CA} \)\[ = \left| {\overrightarrow {AB} .} \right|\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) + \left| {\overrightarrow {CM} } \right|.\left| {\overrightarrow {CA} } \right|.\cos \left( {\overrightarrow {CM} ,\overrightarrow {CA} } \right)\]

\[ = {a^2}.\cos 60^\circ + \frac{{{a^2}}}{2}.\cos 60^\circ = \frac{{3{a^2}}}{4}\].

d) Ta có \(\overrightarrow {AB'} .\overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)\)

\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)

\( = - \overrightarrow {BA} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {BB'} \)

\( = - \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|.\cos \left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) + {\left| {\overrightarrow {BB'} } \right|^2}\)

\( = - {a^2}.\cos 60^\circ + {\left( {a\sqrt 2 } \right)^2}\)

\( = - \frac{{{a^2}}}{2} + {\left( {a\sqrt 2 } \right)^2}\)\( = \frac{{3{a^2}}}{2}\).

Khi đó \(\cos \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} .\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BC'} } \right|}} = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2}\)\( \Rightarrow \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = 60^\circ \).

Đáp án: a) Đúng; b) Đúng; c) Sai; d) Đúng.