Cho biết \(\cos \alpha = - \frac{2}{3}\). Tính giá trị của biểu thức \(E = \frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\).
A. \( - \frac{{19}}{{13}}\).
Quảng cáo
Trả lời:
Ta có \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} \Rightarrow {\tan ^2}\alpha = \frac{1}{{{{\left( { - \frac{2}{3}} \right)}^2}}} - 1 = \frac{9}{4} - 1 = \frac{5}{4}\).
Vậy \(E = \frac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }} = \frac{{\left( {\cot \alpha + 3\tan \alpha } \right)\tan \alpha }}{{\left( {2\cot \alpha + \tan \alpha } \right)\tan \alpha }} = \frac{{1 + 3{{\tan }^2}\alpha }}{{2 + {{\tan }^2}\alpha }} = \frac{{1 + 3 \cdot \frac{5}{4}}}{{2 + \frac{5}{4}}} = \frac{{19}}{{13}}\). Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
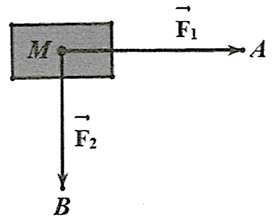
Ta có tổng lực tác dụng lên vật: \({\vec F_1} + {\vec F_2} = \overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MC} \) (với \(C\) là điểm sao cho \(AMBC\) là hình bình hành).
Khi đó cường độ lực tác dụng lên vật: \(\left| {{{\vec F}_1} + {{\vec F}_2}} \right| = \left| {\overrightarrow {MC} } \right| = MC\).
Ta có: \(MA = \left| {\overrightarrow {MA} } \right| = \left| {{{\vec F}_1}} \right| = 400\;{\rm{N}}\), \[MB = \left| {\overrightarrow {MB} } \right| = \left| {{{\vec F}_2}} \right| = 300\;{\rm{N}}\].
Mặt khác, do \(\widehat {AMB} = 90^\circ \) nên \(AMBC\) là hình chữ nhật.
Khi đó \(MC = \sqrt {M{A^2} + M{B^2}} = \sqrt {{{400}^2} + {{300}^2}} = 500\,\,{\rm{(N)}}\).
Vậy cường độ của lực tác động lên vật bằng 500 N.
Câu 2
A. \(x - y \ge 1\).
Lời giải
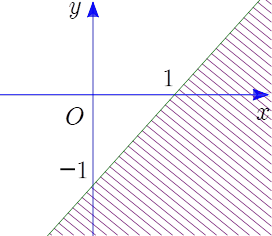
Đường thẳng \(x - y = 1\) đi qua hai điểm \(\left( {0; - 1} \right),\,\,\left( {1;0} \right)\).
Điểm \(O\left( {0;0} \right)\) thuộc miền nghiệm của bất phương trình \(x - y \le 1\).
Vậy bất phương trình có miền nghiệm như hình vẽ là \(x - y \le 1\). Chọn B.
Câu 3
A. \(\forall x \in \mathbb{R}:{x^2} \ge 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow 0 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(A = \left\{ { - 1;0;1;2;3} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.