Trong không gian \(Oxyz\), cho \[\overrightarrow u = \left( {1; - 1;5} \right)\] và \[\overrightarrow v = \left( {2; - 4;7} \right)\]. Tính \(\left[ {\overrightarrow u ,\overrightarrow v } \right]\) ?

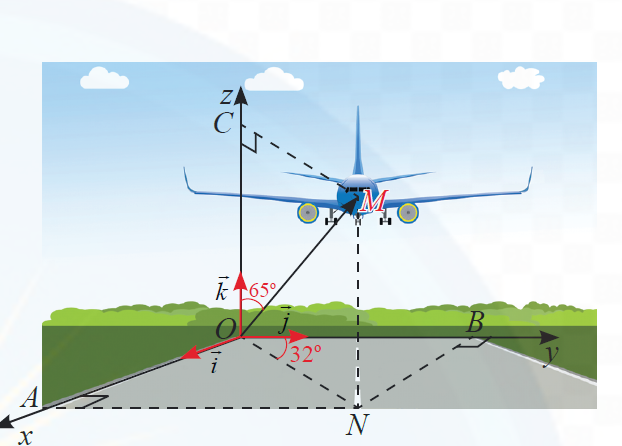
Tam giác \(OCM\) vuông tại \(C\) có

\(OC = OM.\cos 65^\circ  = 14.\cos 65^\circ  \approx 5,9\) và \(CM = OM.\sin 65^\circ  = 14.\sin 65^\circ  \approx 12,7\).

\(ON = CM,\,\,AN = OB\).

Có \(\widehat {AON} = 90^\circ  - \widehat {BON} = 58^\circ \)

Tam giác \(OAN\) vuông tại \(A\) có

\(OA = ON.\cos 58^\circ  = 12,7.\cos 58^\circ  \approx 6,7\) và \(AN = ON.\sin 58^\circ  = 12,7.\sin 58^\circ  \approx 10,8\).

\(\overrightarrow {OM}  = OA.\overrightarrow i  + OB.\overrightarrow j  + OC.\overrightarrow k  = 6,7.\overrightarrow i  + 10,8.\overrightarrow j  + 5,9.\overrightarrow k \).

Vậy \(M\left( {6,7;10,8;5,9} \right)\).

a) Ta có \(A\left( {1; - 2;3} \right),\,\,B\left( { - 2;1;2} \right) \Rightarrow \overrightarrow {AB}  = \left( { - 3;3; - 1} \right)\). Suy ra a) đúng.

b) Ta có \(A\left( {1; - 2;3} \right),\,\,C\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AC}  = \left( {2;1; - 1} \right)\). Suy ra b) sai.

c) Do \(3\overrightarrow {AC}  = \left( {6;3; - 3} \right);\,\overrightarrow {AB}  = \left( { - 3;3; - 1} \right)\). Suy ra c) sai.

d) Ta có\(\overrightarrow {AB}  = \left( { - 3;3; - 1} \right);\,\overrightarrow {AC}  = \left( {2;1; - 1} \right) \Rightarrow \frac{{ - 3}}{2} \ne \frac{3}{1} \Rightarrow \overrightarrow {AB} \), \(\overrightarrow {AC} \) không cùng phương. Suy ra ba điểm \(A,\,B,\,C\) không thẳng hàng. Suy ra d) đúng.