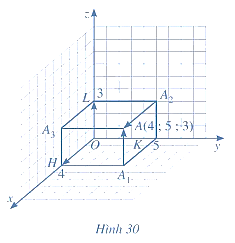
Trong không gian \[Oxyz,\]cho hình hộp \[ABCD.A'B'C'D'\] có \[A\left( {1;0;1} \right),B\left( {2;1;2} \right),D\left( {1; - 1;1} \right)\], \[A'\left( {1;1; - 1} \right)\] và \[B'\left( {{b_1};{b_2};{b_3}} \right)\]. Xét tính đúng sai của các phát biểu sau:

Mệnh đề	Đúng	Sai
a) \(\overrightarrow {A'A} = \left( {0; - 1;2} \right)\).
b) \(\overrightarrow {B'B} = \left( {2 - {b_1};1 - {b_2};2 - {b_3}} \right)\).
c) \(\overrightarrow {A'A} = \overrightarrow {B'B} \).
d) \[B'\left( {2;0;\,0} \right)\]

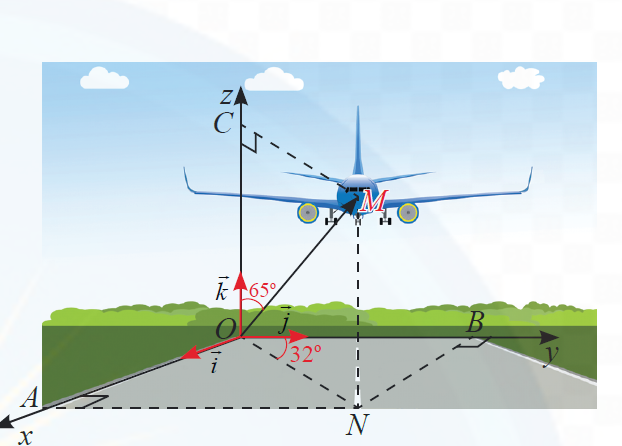
Tam giác \(OCM\) vuông tại \(C\) có

\(OC = OM.\cos 65^\circ  = 14.\cos 65^\circ  \approx 5,9\) và \(CM = OM.\sin 65^\circ  = 14.\sin 65^\circ  \approx 12,7\).

\(ON = CM,\,\,AN = OB\).

Có \(\widehat {AON} = 90^\circ  - \widehat {BON} = 58^\circ \)

Tam giác \(OAN\) vuông tại \(A\) có

\(OA = ON.\cos 58^\circ  = 12,7.\cos 58^\circ  \approx 6,7\) và \(AN = ON.\sin 58^\circ  = 12,7.\sin 58^\circ  \approx 10,8\).

\(\overrightarrow {OM}  = OA.\overrightarrow i  + OB.\overrightarrow j  + OC.\overrightarrow k  = 6,7.\overrightarrow i  + 10,8.\overrightarrow j  + 5,9.\overrightarrow k \).

Vậy \(M\left( {6,7;10,8;5,9} \right)\).

a) Ta có \(A\left( {1; - 2;3} \right),\,\,B\left( { - 2;1;2} \right) \Rightarrow \overrightarrow {AB}  = \left( { - 3;3; - 1} \right)\). Suy ra a) đúng.

b) Ta có \(A\left( {1; - 2;3} \right),\,\,C\left( {3; - 1;2} \right) \Rightarrow \overrightarrow {AC}  = \left( {2;1; - 1} \right)\). Suy ra b) sai.

c) Do \(3\overrightarrow {AC}  = \left( {6;3; - 3} \right);\,\overrightarrow {AB}  = \left( { - 3;3; - 1} \right)\). Suy ra c) sai.

d) Ta có\(\overrightarrow {AB}  = \left( { - 3;3; - 1} \right);\,\overrightarrow {AC}  = \left( {2;1; - 1} \right) \Rightarrow \frac{{ - 3}}{2} \ne \frac{3}{1} \Rightarrow \overrightarrow {AB} \), \(\overrightarrow {AC} \) không cùng phương. Suy ra ba điểm \(A,\,B,\,C\) không thẳng hàng. Suy ra d) đúng.