Cho tứ diện \[ABCD\]. Gọi \[G\] là trọng tâm tam giác \[BCD\] và điểm \[M\] thuộc cạnh \[AB\] sao cho \[AM = 2BM\]. Đẳng thức nào sau đây là đúng?

a) Đúng.

b) Đúng.

Ta có: \(\overrightarrow {C'K}  = \overrightarrow {C'C}  + \overrightarrow {CK}  = \overrightarrow {C'C}  + \frac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CD} } \right) = \overrightarrow {C'C}  + \frac{1}{2}\left( {\overrightarrow {C'A'}  + \overrightarrow {C'D'} } \right)\)

\( = \overrightarrow {C'C}  + \frac{1}{2}\left( {\overrightarrow {C'B'}  + \overrightarrow {C'D'}  + \overrightarrow {C'D'} } \right) = \overrightarrow {C'C}  + \frac{1}{2}\overrightarrow {C'B'}  + \overrightarrow {C'D'} \)

c) Sai.

Ta có: \[\overrightarrow {AB} .\overrightarrow {B'D'}  = \left( {\overrightarrow {AA'}  + \overrightarrow {A'B'}  + \overrightarrow {B'B} } \right).\overrightarrow {B'D'}  = \overrightarrow {AA'} .\overrightarrow {B'D'}  + \overrightarrow {A'B'} .\overrightarrow {B'D'}  + \overrightarrow {B'B} .\overrightarrow {B'D'}  = \overrightarrow {A'B'} .\overrightarrow {B'D'} \]

\( = A'B'.B'D'.{\rm{cos}}\left( {\overrightarrow {A'B'} ,\overrightarrow {B'D'} } \right) = a.a\sqrt 2 .{\rm{cos}}\left( {135^\circ } \right) =  - {a^2}\)

d) Đúng.

Ta đặt \[\overrightarrow {AA'}  = \overrightarrow a ,\overrightarrow {AB}  = \overrightarrow b ,\overrightarrow {AD}  = \overrightarrow c \]. Ta có \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = \left| {\overrightarrow c } \right| = a\]

\[\overrightarrow {AC'}  = \overrightarrow {AA'}  + \overrightarrow {AB}  + \overrightarrow {AD} \] hay \[\overrightarrow {AC'}  = \overrightarrow a  + \overrightarrow b  + \overrightarrow c \]

Mặt khác

\[\overrightarrow {MN}  = \overrightarrow {AN}  - \overrightarrow {AM}  = \left( {\overrightarrow {AB}  + \overrightarrow {BN} } \right) - \left( {\overrightarrow {AD}  + \overrightarrow {DM} } \right)\] với \[\overrightarrow {BN}  = \frac{x}{a}.\overrightarrow a \] và \[\overrightarrow {DM}  = \frac{x}{a}.\overrightarrow b \]

Do đó \[\overrightarrow {MN}  = \left( {\overrightarrow b  + \frac{x}{a}\overrightarrow a } \right) - \left( {\overrightarrow c  + \frac{x}{a}\overrightarrow b } \right) = \frac{x}{a}\overrightarrow a  + \left( {a - \frac{x}{a}} \right)\overrightarrow b  - \overrightarrow c \]

Ta có \[\overrightarrow {AC'} .\overrightarrow {MN}  = \left( {\overrightarrow a  + \overrightarrow b  + \overrightarrow c } \right)\left[ {\frac{x}{a}\overrightarrow a  + \left( {a - \frac{x}{a}} \right)\overrightarrow b  - \overrightarrow c } \right]\]

Vì \[\overrightarrow a .\overrightarrow b  = 0,\overrightarrow a .\overrightarrow c  = 0,\overrightarrow b .\overrightarrow c  = 0\] nên ta có

\[\overrightarrow {AC'} .\overrightarrow {MN}  = \frac{x}{a}{\overrightarrow a ^2} + \left( {1 - \frac{x}{a}} \right){\overrightarrow b ^2} - {\overrightarrow c ^2} = x.a + \left( {1 - \frac{x}{a}} \right){a^2} - {a^2} = 0\], vậy góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng  \(90^\circ \).

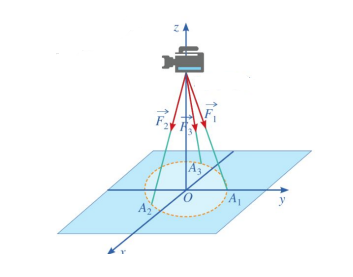
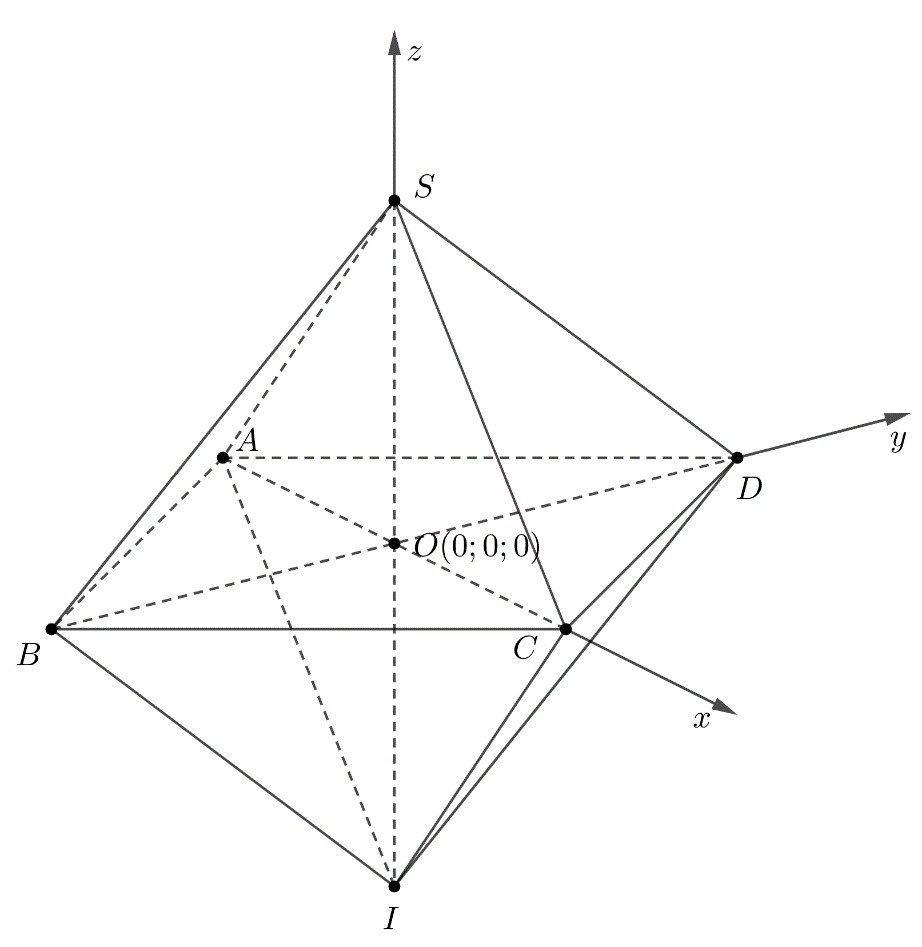
Ta có: \(\overrightarrow {E{A_1}}  = \left( {0;1; - 8} \right)\),\(\overrightarrow {E{A_2}}  = \left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\), \(\overrightarrow {E{A_3}}  = \left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\) Nên \(E{A_1} = E{A_2} = E{A_3} = \sqrt {65} \)

Mặt khác, \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ

Do đó : \(\overrightarrow {{F_1}}  = k\overrightarrow {E{A_1}}  = \left( {0;k; - 8k} \right)\),\[\overrightarrow {{F_2}}  = k\overrightarrow {E{A_2}}  = \left( {\frac{{\sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\],\(\overrightarrow {{F_3}}  = k\overrightarrow {E{A_3}}  = \left( {\frac{{ - \sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\)

\( \Rightarrow {\overrightarrow F _1} + \overrightarrow {{F_2}}  + {\overrightarrow F _3} = \left( {0;0; - 24k} \right)\)

Mà \({\overrightarrow F _1} + \overrightarrow {{F_2}}  + {\overrightarrow F _3} = \overrightarrow P  = \left( {0;0; - 240} \right) \Rightarrow  - 24k =  - 240 \Rightarrow k = 10\)

Vậy \(\overrightarrow {{F_1}}  = \left( {0;10; - 80} \right)\)