Trong một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng \(6m\) và cao \(4m\)có \(2\)cây quạt treo tường. Cây quạt \(A\)treo chính gữa bức tường \(8m\)và cách trần \(1m\), cây quạt \(B\) treo chính giữa bức tường \(6m\)và cách trần \(1,5m\). Chọn hệ trục tọa độ \(Oxyz\)như hình vẽ bên dưới ( đơn vị: mét). Hãy xác định tọa độ của \(\overrightarrow {AB} \).

Trong một căn phòng dạng hình hộp chữ nhật với chiều dài \(8m\), rộng \(6m\) và cao \(4m\)có \(2\)cây quạt treo tường. Cây quạt \(A\)treo chính gữa bức tường \(8m\)và cách trần \(1m\), cây quạt \(B\) treo chính giữa bức tường \(6m\)và cách trần \(1,5m\). Chọn hệ trục tọa độ \(Oxyz\)như hình vẽ bên dưới ( đơn vị: mét). Hãy xác định tọa độ của \(\overrightarrow {AB} \).

Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Từ hình vẽ: \(A \in \left( {Oxz} \right)\) nên \(A\left( {x\,;\,0\,;\,z} \right)\) - \(B \in \left( {Oyz} \right)\) nên \(B\left( {0\,;\,y\,;\,z} \right)\)
Cây quạt \(A\)treo chính giữa bức tường \(8m\)và cách trần \(1m\) nên \(A\left( {4\,;\,0\,;\,3} \right)\).
Cây quạt \(B\) treo chính giữa bức tường \(6m\)và cách trần \(1,5m\) nên \(B\left( {0\,;\,3\,;\,\frac{5}{2}} \right)\).
Khi đó \(\overrightarrow {AB} = \left( {{x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A}} \right) = \left( { - 4\,;\,3\,;\, - \frac{1}{2}} \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng.
b) Đúng.
Ta có: \(\overrightarrow {C'K} = \overrightarrow {C'C} + \overrightarrow {CK} = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CD} } \right) = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'A'} + \overrightarrow {C'D'} } \right)\)
\( = \overrightarrow {C'C} + \frac{1}{2}\left( {\overrightarrow {C'B'} + \overrightarrow {C'D'} + \overrightarrow {C'D'} } \right) = \overrightarrow {C'C} + \frac{1}{2}\overrightarrow {C'B'} + \overrightarrow {C'D'} \)
c) Sai.
Ta có: \[\overrightarrow {AB} .\overrightarrow {B'D'} = \left( {\overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {B'B} } \right).\overrightarrow {B'D'} = \overrightarrow {AA'} .\overrightarrow {B'D'} + \overrightarrow {A'B'} .\overrightarrow {B'D'} + \overrightarrow {B'B} .\overrightarrow {B'D'} = \overrightarrow {A'B'} .\overrightarrow {B'D'} \]
\( = A'B'.B'D'.{\rm{cos}}\left( {\overrightarrow {A'B'} ,\overrightarrow {B'D'} } \right) = a.a\sqrt 2 .{\rm{cos}}\left( {135^\circ } \right) = - {a^2}\)
d) Đúng.
Ta đặt \[\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\overrightarrow {AD} = \overrightarrow c \]. Ta có \[\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right| = \left| {\overrightarrow c } \right| = a\]
\[\overrightarrow {AC'} = \overrightarrow {AA'} + \overrightarrow {AB} + \overrightarrow {AD} \] hay \[\overrightarrow {AC'} = \overrightarrow a + \overrightarrow b + \overrightarrow c \]
Mặt khác
\[\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \left( {\overrightarrow {AB} + \overrightarrow {BN} } \right) - \left( {\overrightarrow {AD} + \overrightarrow {DM} } \right)\] với \[\overrightarrow {BN} = \frac{x}{a}.\overrightarrow a \] và \[\overrightarrow {DM} = \frac{x}{a}.\overrightarrow b \]
Do đó \[\overrightarrow {MN} = \left( {\overrightarrow b + \frac{x}{a}\overrightarrow a } \right) - \left( {\overrightarrow c + \frac{x}{a}\overrightarrow b } \right) = \frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c \]
Ta có \[\overrightarrow {AC'} .\overrightarrow {MN} = \left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\left[ {\frac{x}{a}\overrightarrow a + \left( {a - \frac{x}{a}} \right)\overrightarrow b - \overrightarrow c } \right]\]
Vì \[\overrightarrow a .\overrightarrow b = 0,\overrightarrow a .\overrightarrow c = 0,\overrightarrow b .\overrightarrow c = 0\] nên ta có
\[\overrightarrow {AC'} .\overrightarrow {MN} = \frac{x}{a}{\overrightarrow a ^2} + \left( {1 - \frac{x}{a}} \right){\overrightarrow b ^2} - {\overrightarrow c ^2} = x.a + \left( {1 - \frac{x}{a}} \right){a^2} - {a^2} = 0\], vậy góc giữa vectơ \[\overrightarrow {AC'} \] và \(\overrightarrow {MN} \) bằng \(90^\circ \).
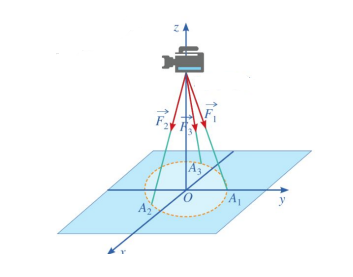
Câu 2
Lời giải
Ta có: \(\overrightarrow {E{A_1}} = \left( {0;1; - 8} \right)\),\(\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\), \(\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2};\frac{{ - 1}}{2}; - 8} \right)\) Nên \(E{A_1} = E{A_2} = E{A_3} = \sqrt {65} \)
Mặt khác, \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ
Do đó : \(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} = \left( {0;k; - 8k} \right)\),\[\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} = \left( {\frac{{\sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\],\(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} = \left( {\frac{{ - \sqrt 3 }}{2}k;\frac{{ - 1}}{2}k; - 8k} \right)\)
\( \Rightarrow {\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \left( {0;0; - 24k} \right)\)
Mà \({\overrightarrow F _1} + \overrightarrow {{F_2}} + {\overrightarrow F _3} = \overrightarrow P = \left( {0;0; - 240} \right) \Rightarrow - 24k = - 240 \Rightarrow k = 10\)
Vậy \(\overrightarrow {{F_1}} = \left( {0;10; - 80} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.