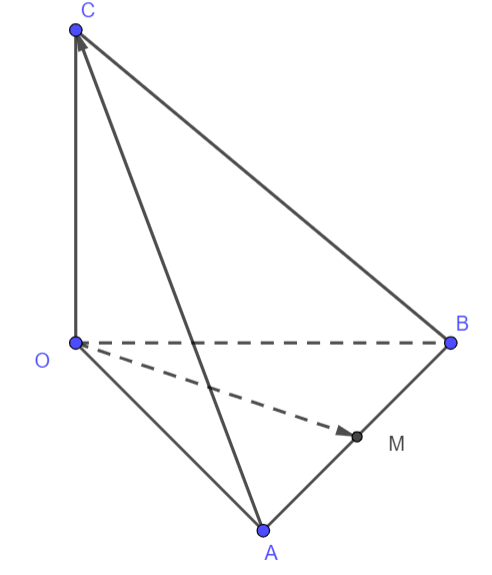
Trong không gian tọa độ Oxyz cho 2 điểm \(\,B\left( {2;1;0} \right);\,\,C\left( {1;4;5} \right).\)Điểm \(M(x;y;z)\) thuộc trục hoành sao cho \(MB = MC\). Khi đó giá trị \(2x + y + z\)bằng bao nhiêu?
Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Do điểm \(M \in {\rm{Ox}}\) nên ta gọi \(M\left( {x;0;0} \right)\) ta có \(MB = MC \Leftrightarrow M{B^2} = M{C^2}\).
\( \Leftrightarrow {\left( {x - 2} \right)^2} + {1^2} + {0^2} = {\left( {x - 1} \right)^2} + {4^2} + {5^2} \Leftrightarrow {x^2} - 4{\rm{x}} + 5 = {x^2} - 2{\rm{x}} + 42 \Leftrightarrow x = \frac{{ - 37}}{2}.\)
Vậy \(M\left( { - \frac{{37}}{2};0;0} \right) \Rightarrow \,2x + y + z = - 37\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
ĐS: \(3,74\).
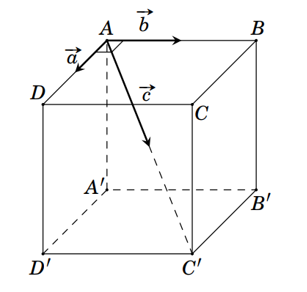
Ta có: \[{\left| {\vec a + \vec b} \right|^2} = {\left( {\vec a + \vec b} \right)^2} = {\left| {\vec a} \right|^2} + 2\vec a\vec b + {\left| {\vec b} \right|^2}\]\( \Rightarrow 2\vec a\vec b = {\left| {\vec a + \vec b} \right|^2} - {\left| {\vec a} \right|^2} - {\left| {\vec b} \right|^2} = 11\).
\[{\left| {\vec a - \vec b} \right|^2} = {\left( {\vec a - \vec b} \right)^2} = {\left| {\vec a} \right|^2} - 2\vec a\vec b + {\left| {\vec b} \right|^2} = 9 - 11 + 16 = 14\]\( \Rightarrow \left| {\vec a - \vec b} \right| = \sqrt {14} \approx 3,74\).
Lời giải
a) Đ
b) S
c) Đ
Gọi \(D\left( {x;\,\,y} \right)\). Khi đó , \(\overrightarrow {DC} = \left( {1 - x;\,\,1 - y;\, - 2 - z\,} \right)\)
Vì \(ABCD\)là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left\{ \begin{array}{l} - 3 = 1 - x\\ - 1 = 1 - y\\ - 1 = - 2 - z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 4\\y = 2\\z = - 1\end{array} \right.\)
Vậy \(D\left( {4;\,\,2;\,\, - 1} \right)\)
d) Đ
Gọi \(H\left( {x;y;z} \right)\) là trực tâm tam giác \(ABC\).
Khi đó tọa độ điểm \(H\) thỏa mãn \( \Leftrightarrow \)\(\left\{ \begin{array}{l}\overrightarrow {AH} .\overrightarrow {BC} = 0\\\overrightarrow {BH} .\overrightarrow {AC} = 0\\\left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right].\overrightarrow {AH} \, = 0\end{array} \right.\)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}2x - y - 2z = - 1\\x + 2y + 3z = 3\\x - 8y + 5z = - 17\end{array} \right.\).
Suy ra \(H\left( {\frac{2}{{15}};\frac{{29}}{{15}}; - \frac{1}{3}} \right)\).
Vậy \[OH = \frac{{\sqrt {870} }}{{15}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(M\left( { - 4;0;0} \right).\)
B. \(M\left( {5;0;0} \right).\)
C. \(M\left( {4;0;0} \right).\)
D. \(M\left( { - 5;0;0} \right).\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập