Hình bên dưới mô tả một hồ bơi theo tiêu chuẩn với kích thước như hình vẽ và biết chiều sâu của hồ bơi là 2 m. Biết hồ bơi này có 10 làn bơi với độ rộng như nhau và mỗi làn bơi được ngăn cách bằng phao ngăn phân làn nổi trên mặt nước. Chọn hệ trục \(Oxyz\) như hình bên dưới sao cho gốc tọa độ \(O\) nằm ở dưới đáy của hồ và chiều của vectơ \[\overrightarrow k \] hướng dọc thẳng đứng lên từ đáy bể lên miệng bể. Gọi \(AB\) là là phao ngăn phân làn như hình vẽ và có độ dài là 40 m. Biết hai điểm \(A\) và \(B\) cách đều hai bên thành hồ ứng với chiều rộng của hồ. Hãy xác định tọa độ của vectơ \(\overrightarrow {AB} \).

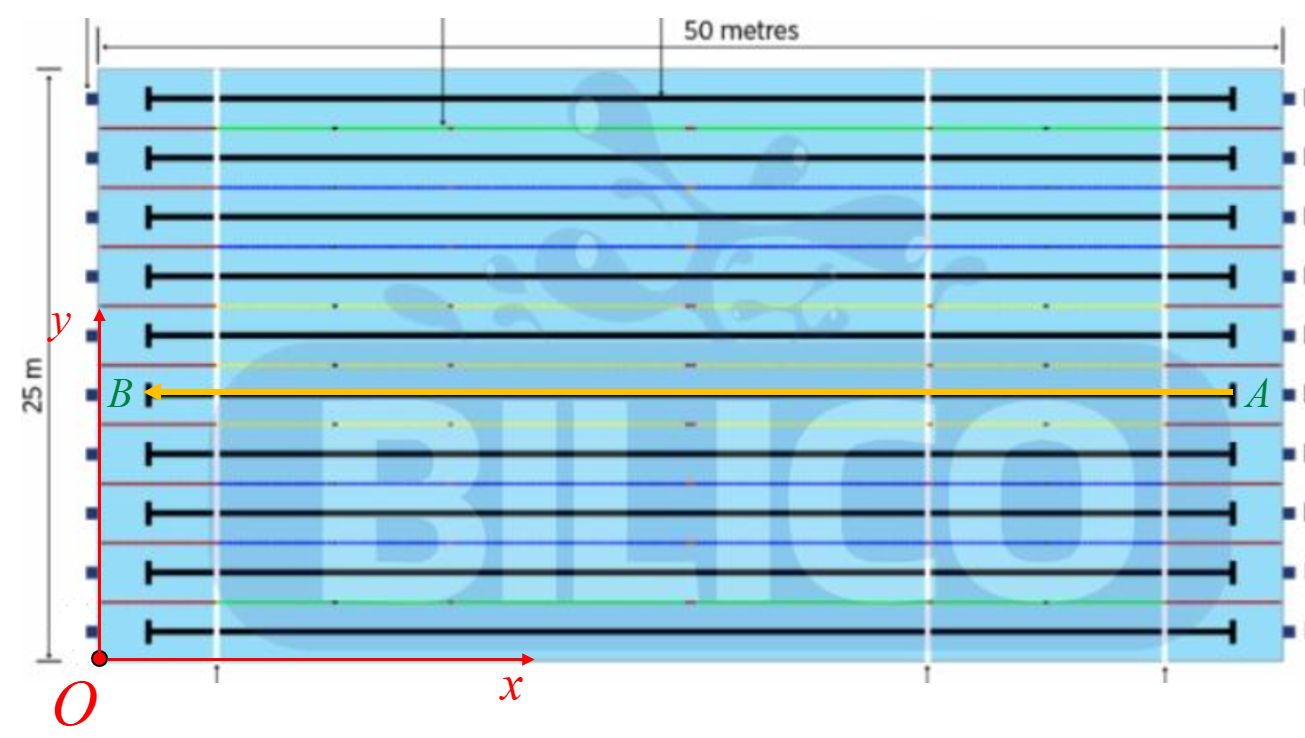
Hình bên dưới mô tả một hồ bơi theo tiêu chuẩn với kích thước như hình vẽ và biết chiều sâu của hồ bơi là 2 m. Biết hồ bơi này có 10 làn bơi với độ rộng như nhau và mỗi làn bơi được ngăn cách bằng phao ngăn phân làn nổi trên mặt nước. Chọn hệ trục \(Oxyz\) như hình bên dưới sao cho gốc tọa độ \(O\) nằm ở dưới đáy của hồ và chiều của vectơ \[\overrightarrow k \] hướng dọc thẳng đứng lên từ đáy bể lên miệng bể. Gọi \(AB\) là là phao ngăn phân làn như hình vẽ và có độ dài là 40 m. Biết hai điểm \(A\) và \(B\) cách đều hai bên thành hồ ứng với chiều rộng của hồ. Hãy xác định tọa độ của vectơ \(\overrightarrow {AB} \).


Câu hỏi trong đề: Đề kiểm tra Ôn tập cuối chương 2 (có lời giải) !!
Quảng cáo
Trả lời:
Đáp số: \(\overrightarrow {AB} = \left( {0;\,\, - 40;\,\,0} \right)\).
Gọi tọa độ điểm \(A\) và \(B\) lần lượt là \(\left( {{x_A};\,{y_A};\,{z_A}} \right)\) và \(\left( {{x_B};\,{y_B};\,{z_B}} \right)\). Do hồ bơi này có chiều rộng là 25 m và có 10 làn bơi với độ rộng như nhau nên độ rộng mỗi làn bơi là: \(25:10 = 2,5\,\,{\rm{m}}\).
Do phao ngăn phân làn \(AB\) nằm giữa làn thứ 5 trong hình tính từ dưới lên trên.
Suy ra: \(AB\) cách thành hồ là giá của vectơ \(\overrightarrow i \) ứng với trục \(Ox\) là \(2,5.4 + 2,5:2 = 11,25\,\,{\rm{m}}\).
Do AB song song với giá của vectơ \(Ox\) nên: \[{y_A} = {y_B} = 11,25\].
Ta lại có hai điểm \(A\) và \(B\) đều cách đều hai bên thành hồ ứng với chiều rộng của hồ và \(AB = 40\,{\rm{m}}\).
Suy ra: điểm B cách thành hồ là giá của vectơ \(\overrightarrow j \) ứng với trục \(Oy\) là: \(\left( {50 - 40} \right):2 = 5\,\,{\rm{m}}\).
Suy ra: \({x_B} = 5\) và \({x_A} = 45\).
Do phao ngăn phân làn nổi trên mặt hồ và cách đáy hồ 2 m nên: \({z_B} = {z_A} = 2\).
Suy ra: \(A\left( {11,25;\,\,45;\,\,2} \right)\) và \(B\left( {11,25;\,\,5;\,\,2} \right)\).
Vậy tọa độ của vectơ \(\overrightarrow {AB} \) là: \(\overrightarrow {AB} = \left( {11,25 - 11,25;\,\,5 - 45;\,\,2 - 2} \right) = \left( {0;\,\, - 40;\,\,0} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
![Cho hình lăng trụ tam giác đều ABC.A'B'C' có \[AB = a\] và \[AA' = a\sqrt 2 \]. Các mệnh đề dưới đây đúng hay sai? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/3-1759377354.png)
a) Đúng.
b) Đúng.
Ta có: \(\overrightarrow {A'A} + \overrightarrow {A'B'} - \overrightarrow {CM} = \overrightarrow {A'A} + \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {A'B} + \overrightarrow {BM} = \overrightarrow {A'M} \)
c) Sai.
Ta có: \(\overrightarrow {A'M} .\overrightarrow {AC} = \left( {\overrightarrow {A'A} + \overrightarrow {AM} } \right).\overrightarrow {AC} = \overrightarrow {A'A} .\overrightarrow {AC} + \overrightarrow {AM} .\overrightarrow {AC} = \overrightarrow {AM} .\overrightarrow {AC} = \frac{{a\sqrt 3 }}{2}.a.\cos 30^\circ = \frac{{3{a^2}}}{4}\)
d) Đúng.
Ta có \(\overrightarrow {AB'} .\overrightarrow {BC'} = \left( {\overrightarrow {AB} + \overrightarrow {BB'} } \right)\left( {\overrightarrow {BC} + \overrightarrow {CC'} } \right)\)\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)
\( = \overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {AB} .\overrightarrow {CC'} + \overrightarrow {BB'} .\overrightarrow {BC} + \overrightarrow {BB'} .\overrightarrow {CC'} \)\( = - \frac{{{a^2}}}{2} + 0 + 0 + 2{a^2} = \frac{{3{a^2}}}{2}\)
Suy ra \(\cos \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = \frac{{\overrightarrow {AB'} .\overrightarrow {BC'} }}{{\left| {\overrightarrow {AB'} } \right|.\left| {\overrightarrow {BC'} } \right|}}\)\( = \frac{{\frac{{3{a^2}}}{2}}}{{a\sqrt 3 .a\sqrt 3 }} = \frac{1}{2} \Rightarrow \left( {\overrightarrow {AB'} ,\overrightarrow {BC'} } \right) = 60^\circ \)
Lời giải
a) Đúng.
\(\overrightarrow {AB} = \left( {1;3; - 2} \right)\).
b) Đúng.
\(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = 1\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{2}{3}\\{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{2}{3}\end{array} \right.\).
c) Sai.
Tọa độ hình chiếu của điểm \(B\left( {2;1; - 2} \right)\) trên mặt phẳng \(Oxy\) là \(H\left( {2;1;0} \right)\).
d) Sai.
\(\overrightarrow {AB} = \left( {1;3; - 2} \right) \Rightarrow 2\overrightarrow {AB} = \left( {2;6; - 4} \right)\)
\(\overrightarrow {BC} = \left( { - 2;2;6} \right) \Rightarrow - 3\overrightarrow {BC} = \left( {6; - 6; - 18} \right)\)
Vậy \(\overrightarrow x = \left( {8;0; - 22} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.