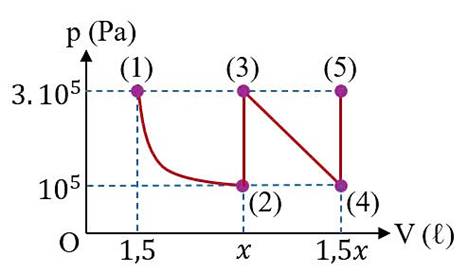
Một khối khí lí tưởng xác định thực hiện chu trình gồm các trạng thái (1) → (2) → (3) → (4) → (5). Đồ thị biểu diễn quá trình (1) → (2) là một đường hyperbol. Nhiệt độ của khối khí ở trạng thái (1) là 27 °C.
a) Số mol của khối khí lí tưởng xấp xỉ bằng 0,18 mol.
b) Thể tích của khối khí ở trạng thái (2) bằng $4,5·10^{-3} m^3$.
c) Khi khối khí biến đổi từ trạng thái (2) sang trạng thái (3), động năng tịnh tiến trung bình của mỗi phân tử khí tăng 3 lần.
d) Nhiệt độ của khối khí ở trạng thái (5) là 300 K.
Một khối khí lí tưởng xác định thực hiện chu trình gồm các trạng thái (1) → (2) → (3) → (4) → (5). Đồ thị biểu diễn quá trình (1) → (2) là một đường hyperbol. Nhiệt độ của khối khí ở trạng thái (1) là 27 °C.
a) Số mol của khối khí lí tưởng xấp xỉ bằng 0,18 mol.
b) Thể tích của khối khí ở trạng thái (2) bằng $4,5·10^{-3} m^3$.
c) Khi khối khí biến đổi từ trạng thái (2) sang trạng thái (3), động năng tịnh tiến trung bình của mỗi phân tử khí tăng 3 lần.
d) Nhiệt độ của khối khí ở trạng thái (5) là 300 K.
b) Thể tích của khối khí ở trạng thái (2) bằng $4,5·10^{-3} m^3$.
c) Khi khối khí biến đổi từ trạng thái (2) sang trạng thái (3), động năng tịnh tiến trung bình của mỗi phân tử khí tăng 3 lần.
d) Nhiệt độ của khối khí ở trạng thái (5) là 300 K.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
|
Nội dung |
Đúng |
Sai |
|
a |
Số mol của khối khí lí tưởng xấp xỉ bằng 0,18 mol. |
Đ |
|
|
b |
Thể tích của khối khí ở trạng thái (2) bằng 4,5. . |
Đ |
|
|
c |
Khi khối khí biến đổi từ trạng thái (2) sang trạng thái (3), động năng tịnh tiến trung bình của mỗi phân tử khí tăng 3 lần. |
Đ |
|
|
d |
Nhiệt độ của khối khí ở trạng thái (5) là 300 K. |
|
S |
a) ĐÚNG
Từ phương trình trạng thái:
\[
p_1V_1=nRT_1 \Rightarrow
n=\frac{p_1V_1}{RT_1}
=\frac{3\cdot 10^{5}\cdot 1{,}5\cdot 10^{-3}}{8{,}31\cdot(27+273)}
=\frac{50}{277}\approx 0{,}18\ \text{mol}.
\]
b) ĐÚNG
(1) → (2) là đẳng nhiệt nên \(p_1V_1=p_2V_2\):
\[
V_2=\frac{p_1V_1}{p_2}
=\frac{3\cdot 10^{5}\cdot 1{,}5\cdot 10^{-3}}{10^{5}}
=4{,}5\cdot 10^{-3}\ \text{m}^3.
\]
c) ĐÚNG
(2) → (3) là đẳng tích ⇒ \(T\propto p\):
\[
\frac{T_3}{T_2}=\frac{p_3}{p_2}=\frac{3\cdot 10^{5}}{10^{5}}=3.
\]
Mà \(\bar E_t=\tfrac{3}{2}kT\) ⇒ động năng tịnh tiến trung bình tăng 3 lần.
d) SAI
Từ (b) có \(x=V_2=4{,}5\cdot 10^{-3}\ \text{m}^3\). Suy ra
\[
V_5=1{,}5x=6{,}75\cdot 10^{-3}\ \text{m}^3,\quad
T_5=\frac{p_5V_5}{nR}
=\frac{3\cdot 10^{5}\cdot 6{,}75\cdot 10^{-3}}{(50/277)\cdot 8{,}31}
\approx 1{,}35\cdot 10^{3}\ \text{K} \ne 300\ \text{K}.
\]
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là B
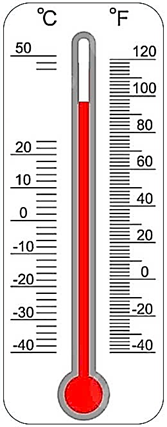
Vì thủy ngân giãn nở tuyến tính theo nhiệt độ, nên khi nhiệt độ tăng thêm $1^\circ\text{C}$ thì chiều dài cột thủy ngân tăng một đoạn
\[
\Delta \ell_{1^\circ\text{C}}=\frac{6{,}25}{50}=0{,}125\ \text{cm}.
\]
Khoảng cách từ vạch $0^\circ\text{C}$ đến mức thủy ngân là $4{,}5\ \text{cm}$, do đó nhiệt độ là
\[
t=\frac{4{,}5}{0{,}125}=36^\circ\text{C}.
\]
Lời giải
Tại thời điểm xác lập kỉ lục Việt Nam, ta có:
\(H_t = H_0\cdot 2^{-\frac{t}{T}} \Rightarrow 0{,}94\,H_0 = H_0\cdot 2^{-\frac{t}{5730}}\Rightarrow t \approx 500\ \text{năm}.\)
\(H_t = H_0\cdot 2^{-\frac{t}{T}} \Rightarrow 0{,}94\,H_0 = H_0\cdot 2^{-\frac{t}{5730}}\Rightarrow t \approx 500\ \text{năm}.\)
Câu 3
A. 90°C.
B. 80°C.
C. 70°C.
D. 85°C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. $1{,}25\cdot 10^{-7}$ (T).
B. $2{,}5\cdot 10^{-5}$ (T).
C. $3{,}75\cdot 10^{-5}$ (T).
D. $1{,}25\cdot 10^{-5}$ (T).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. nhận một công bằng 270 J.
B. nhận một công bằng 70 J.
C. thực hiện một công bằng 70 J.
D. thực hiện một công bằng 270 J.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 400 J.
B. 504 J.
C. 104 J.
D. 296 J.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
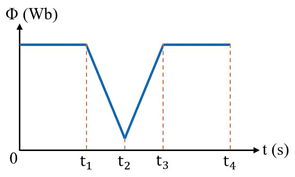
A. Từ t = 0 đến t = t2.
B. Từ t = t1 đến t = t2.
C. Từ t = t2 đến t = t4.
D. Từ t = 0 đến t = t1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập