Phần 2. Trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Một xe ô tô đang chạy với tốc độ \[65\,{\rm{km/h}}\]thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó \[50\,{\rm{m}}\]. Người lái xe phản ứng một giây, sau đó đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ \[v\left( t \right) = - 10t + 20\,\left( {{\rm{m/s}}} \right)\], trong đó \[t\] là thời gian tính bằng giây kể từ lúc đạp phanh. Gọi \[S\left( t \right)\] là quãng đường ô tô đi được trong \[t\] (giây) kể từ lúc đạp phanh.

a) Quãng đường \[S\left( t \right)\] mà xe ô tô đi được trong thời gian \[t\] (giây) là một nguyên hàm của hàm số \[v\left( t \right)\].

b) \[S\left( t \right) = - 5{t^2} + 20t\].

c) Thời gian kể từ lúc đạp phanh đến khi xe ô tô dừng hẳn là 20 giây.

d) Xe ô tô đó không va chạm vào chướng ngại vật trên đường.

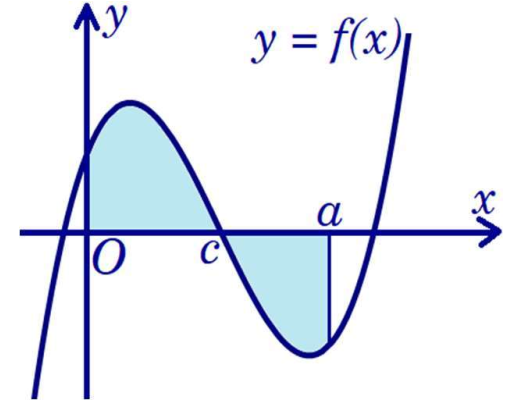
Chọn A

Diện tích hình phẳng: \[S = \int\limits_0^a {\left| {f\left( x \right)} \right|{\rm{d}}x}  = \int\limits_0^c {\left| {f\left( x \right)} \right|{\rm{d}}x}  + \int\limits_c^a {\left| {f\left( x \right)} \right|{\rm{d}}x}  = \int\limits_0^c {f\left( x \right){\rm{d}}x}  - \int\limits_a^c {f\left( x \right){\rm{d}}x} \].

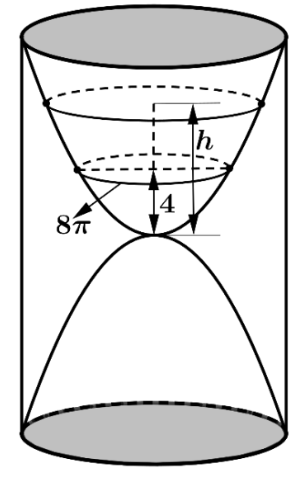
a) Đúng. Ta có \(V\left( t \right) = \int {V'\left( t \right){\rm{d}}t = \int {k.\sqrt t {\rm{d}}t} } \).

Vậy hàm số \(V\left( t \right)\) là một nguyên hàm của hàm số \(f\left( t \right) = k.\sqrt t \).

b) Đúng. Ta có \(V\left( t \right) = \int {V'\left( t \right){\rm{d}}t = \int {k.\sqrt t {\rm{d}}t} }  = \frac{{2k}}{3}.t\sqrt t  + C\), với \(0 \le t \le 24\) và \(k,\,\,C\) là các hằng số.

c) Sai. Do ban đầu bể chứa dầu ban đầu có \(50000\) lít dầu nên \(V\left( 0 \right) = 50\,000 \Rightarrow C = 50\,000\).

Mặt khác sau 4 giờ bơm liên tục, thể tích dầu trong bể đạt \(58000\) lít nên ta có:

\(V\left( 4 \right) = \frac{{2k}}{3}.4\sqrt 4  + 50000 = 58000 \Leftrightarrow k = 1500\).

Vậy \(V\left( t \right) = 1\,000.t\sqrt t  + 50\,000\).

Sau 16 giờ bơm liên tục, thể tích dầu trong bể đạt được:

\(V\left( {16} \right) = 1\,000.16\sqrt 6  + 50\,000 = 114\,000\) lít.

d) Đúng. Trong quá trình bơm dầu, nếu sau mỗi giờ lượng dầu bị rò rỉ đều đặn với tốc độ \(500\) lít/giờ, thì tại thời điểm \(t\) bằng 9 giờ, thể tích dầu trong bể là

\(V\left( 9 \right) = 1\,000.9\sqrt 9  + 50\,000 - 500.9 = 72\,500\) lít.