Một cái cổng hình Parabol như hình vẽ sau:

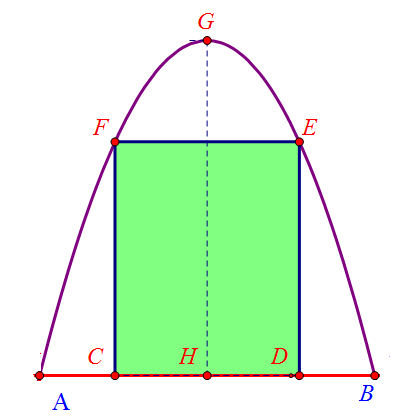
Chiều cao \(GH = 4\,{\rm{m}}\), chiều rộng \(AB = 4\,{\rm{m}}\), \(AC = BD = 0,9\,{\rm{m}}\). Chủ nhà làm hai cánh cổng nhựa lõi thép UPVC, khi đóng lại là hình chữ nhật \(CDEF\) tô đậm có giá là \(1\,500\,000\) đồng/m2, còn các phần để trắng làm xiên hoa có giá là \(1\,000\,000\) đồng/m2. Tổng số tiền để làm hai phần nói trên là bao nhiêu triệu đồng? (kết quả làm tròn đến hàng phần chục).

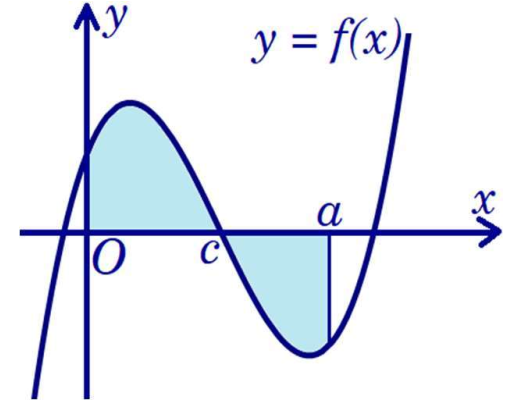
Chọn A

Diện tích hình phẳng: \[S = \int\limits_0^a {\left| {f\left( x \right)} \right|{\rm{d}}x}  = \int\limits_0^c {\left| {f\left( x \right)} \right|{\rm{d}}x}  + \int\limits_c^a {\left| {f\left( x \right)} \right|{\rm{d}}x}  = \int\limits_0^c {f\left( x \right){\rm{d}}x}  - \int\limits_a^c {f\left( x \right){\rm{d}}x} \].

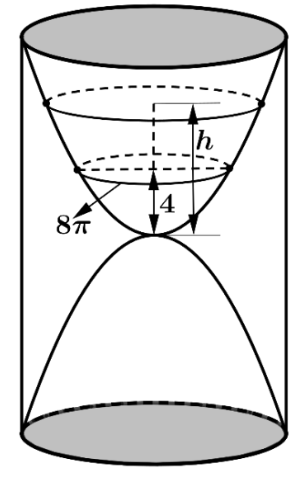
a) Đúng. Ta có \(V\left( t \right) = \int {V'\left( t \right){\rm{d}}t = \int {k.\sqrt t {\rm{d}}t} } \).

Vậy hàm số \(V\left( t \right)\) là một nguyên hàm của hàm số \(f\left( t \right) = k.\sqrt t \).

b) Đúng. Ta có \(V\left( t \right) = \int {V'\left( t \right){\rm{d}}t = \int {k.\sqrt t {\rm{d}}t} }  = \frac{{2k}}{3}.t\sqrt t  + C\), với \(0 \le t \le 24\) và \(k,\,\,C\) là các hằng số.

c) Sai. Do ban đầu bể chứa dầu ban đầu có \(50000\) lít dầu nên \(V\left( 0 \right) = 50\,000 \Rightarrow C = 50\,000\).

Mặt khác sau 4 giờ bơm liên tục, thể tích dầu trong bể đạt \(58000\) lít nên ta có:

\(V\left( 4 \right) = \frac{{2k}}{3}.4\sqrt 4  + 50000 = 58000 \Leftrightarrow k = 1500\).

Vậy \(V\left( t \right) = 1\,000.t\sqrt t  + 50\,000\).

Sau 16 giờ bơm liên tục, thể tích dầu trong bể đạt được:

\(V\left( {16} \right) = 1\,000.16\sqrt 6  + 50\,000 = 114\,000\) lít.

d) Đúng. Trong quá trình bơm dầu, nếu sau mỗi giờ lượng dầu bị rò rỉ đều đặn với tốc độ \(500\) lít/giờ, thì tại thời điểm \(t\) bằng 9 giờ, thể tích dầu trong bể là

\(V\left( 9 \right) = 1\,000.9\sqrt 9  + 50\,000 - 500.9 = 72\,500\) lít.