Để chuẩn bị cho buổi liên hoan của gia đình, bác Ngọc mua hai loại thực phẩm là thịt lợn và cá chép. Giá tiền thịt lợn là \(130\) nghìn đồng/kg, giá tiền cá chép là \(50\) nghìn đồng/kg. Bác Ngọc đã chi \(295\) nghìn để mua \(3,5\,\,{\rm{kg}}\) hai loại thực phẩm trên. Gọi \(x\) và \(y\) lần lượt là số kilogam thịt lợn và cá chép mà bác Ngọc đã mua. Hệ phương trình bậc nhất hai ẩn \(x\) và \(y\) là
A. \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295\end{array} \right.\).
B. \(\left\{ \begin{array}{l}x - y = 3,5\\130x + y = 295\end{array} \right.\).
Quảng cáo
Trả lời:
Chọn A
Gọi \(x\) và \(y\) lần lượt là số kilogam thịt lợn và cá chép mà bác Ngọc đã mua.
Do bác Ngọc chỉ mua \(3,5\,\,{\rm{kg}}\) hai loại thực phẩm trên.
Ta có phương trình: \(x + y = 3,5\).
Giá tiền thịt lợn là \(130\) nghìn đồng/kg, giá tiền cá chép là \(50\) nghìn đồng/kg.
Bác Ngọc đã chi \(295\) nghìn để mua \(3,5\,\,{\rm{kg}}\) hai loại thực phẩm trên.
Ta có phương trình: \(130x + 50y = 295\).
Vậy ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 3,5\\130x + 50y = 295\end{array} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Đúng. Phương trình \(x - y = m + 1\) là phương trình bậc nhất hai ẩn với \(a = 1\,;\,\,b = - 1\,;\,\,c = m + 1\)(\(m\) là tham số).
b) Sai. Với \(m = 2\) ta có hệ phương trình \(\left\{ \begin{array}{l}x - y = 3\\2x + y = 12\end{array} \right.\).
Cộng vế theo vế của hai phương trình của hệ mới, ta được \(3x = 15\) nên \(x = 5\).
Từ đó \(5 - y = 3\) nên \(y = 2\).
Vậy nghiệm của hệ phương trình khi \(m = 2\) là \((x\,;\,\,y) = \left( {5\,;\,\,2} \right).\)
c) Đúng. Cộng vế theo vế của hai phương trình của hệ đã cho, ta được \(3x = 6m + 3\) nên \(x = 2m + 1.\)
Từ đó \(2m + 1 - y = m + 1\) nên \(y = \left( {2m + 1} \right) - \left( {m + 1} \right) = m.\)
d) Đúng. Để hệ phương trình có nghiệm thỏa mãn \(x > 1\,;\,\,y < 2\) thì
\(\left\{ \begin{array}{l}2m + 1 > 1\\m < 2\end{array} \right.\) nên \(\left\{ \begin{array}{l}m > 0\\m < 2\end{array} \right.\) hay \(0 < m < 2\).Lời giải
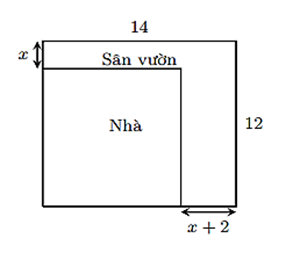
Diện tích làm nhà là: \[\left( {12 - x} \right)\left[ {14 - \left( {x + 2} \right)} \right] = \left( {12 - x} \right)\left( {12 - x} \right)\,\,\,({{\rm{m}}^{\rm{2}}})\] (điều kiện \(0 < x < 12\)).
Vì diện tích đất làm nhà là \(100\,\,{{\rm{m}}^{\rm{2}}}\) nên ta có phương trình
\(\left( {12 - x} \right)\left( {12 - x} \right)\, = 100\)
\({\left( {12 - x} \right)^2} - {10^2} = 0\)
\(\left( {12 - x - 10} \right)\left( {12 - x + 10} \right) = 0\)
\(\left( {2 - x} \right)\left( {22 - x} \right) = 0\)
\(2 - x = 0\) hoặc \(22 - x = 0\)
\(x = 2\) (TMĐK) hoặc \(x = 22\) (loại)
Vậy \(x = 2\,\,{\rm{m}}\).
Đáp án: 2Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.