Trong không gian với hệ toạ độ \(Oxyz\), cho hai điểm \(A\left( {1\,;2\,;3} \right),\,\,B\left( { - 2\,; - 4\,;9} \right)\). Điểm \(M\) thuộc đoạn \(AB\) sao cho \(MA = 2MB\). Độ dài đoạn thẳng \(OM\) là
\(5\).
\(3\).
\(\sqrt {54} \).
\(\sqrt {17} \).
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng: C
Đặt \(M\left( {x\,;y\,;z} \right)\), khi đó: \(\overrightarrow {MA} = \left( {1 - x\,;2 - y\,;3 - z} \right)\) và \(\overrightarrow {MB} = \left( { - 2 - x\,; - 4 - y\,;9 - z} \right)\).
Ta có: \(MA = 2MB \Rightarrow \overrightarrow {MA} = - 2\overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}1 - x = - 2\left( { - 2 - x} \right)\\2 - y = - 2\left( { - 4 - y} \right)\\3 - z = - 2\left( {9 - z} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 1\\y = - 2\\z = 7\end{array} \right. \Rightarrow M\left( { - 1\,; - 2\,;7} \right)\).
Khi đó: \(\overrightarrow {OM} = \left( { - 1\,; - 2\,;7} \right)\). Vậy \[OM = \sqrt {54} \].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
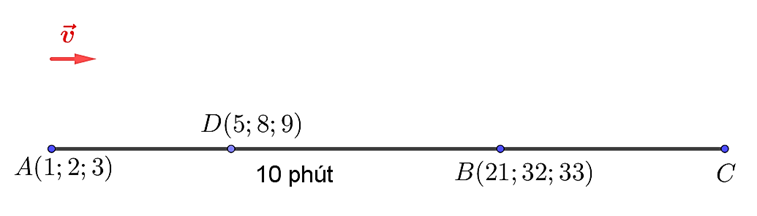
a) Sai.\(\overrightarrow {AB} = \left( {20;\,30;\,30} \right)\); \(\overrightarrow {AD} = \left( {4;\,6;\,6} \right)\).
Ta có \(\frac{{20}}{4} = \frac{{30}}{6} = \frac{{30}}{6}\).
Suy ra \(\overrightarrow {AB} \), \(\overrightarrow {AD} \) cùng phương.
\( \Rightarrow \) 3 điểm \(A\), \(B\), \(D\) thẳng hàng.
Do đó flycam bay qua vị trí \[D\left( {5;\,8;\,9} \right)\].
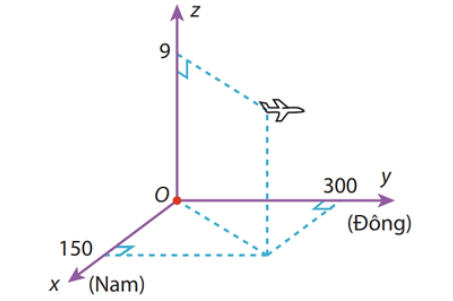
b) Sai.Flycam ở vị trí \(A\left( {1;\,2;\,3} \right)\) và sau 10 phút nó ở vị trí \(B\left( {21;\,32;\,33} \right)\).
\( \Rightarrow \)\(\overrightarrow {AB} = 10\overrightarrow v \)\( \Leftrightarrow \overrightarrow v = \frac{{\overrightarrow {AB} }}{{10}} = \left( {2;\,3;\,3} \right)\).
c) Đúng. Độ lớn của vận tốc flycam là \(\left| {\overrightarrow v } \right| = \sqrt {{2^2} + {3^2} + {3^2}} = \sqrt {22} \)(m/phút).
d) Đúng.Tại thời điểm \(t = 0\), flycam ở vị trí \(A\) và sau 15 phút flycam ở vị trí \(C\).
Suy ra \(\overrightarrow {AC} = 15\overrightarrow v \)\( \Leftrightarrow \left( {{x_C} - 1;\,{y_C} - 2;\,{z_C} - 3} \right) = 15\left( {2;\,3;\,3} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 31\\{y_C} = 47\\{z_C} = 48\end{array} \right.\).
Vậy \(C\left( {31;\,47;\,48} \right)\).
Lời giải
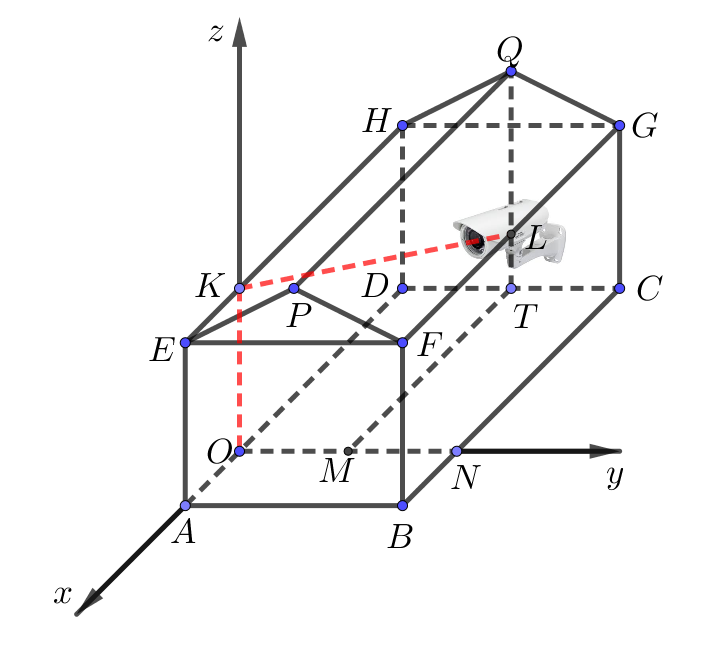
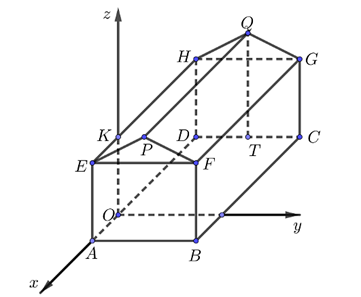
a) Sai. Kẻ \(TM \bot Oy\), \(CN \bot Oy\).
Vì \(T\) là hình chiếu của \(Q\) lên \(\left( {Oxy} \right)\) nên
\(\left\{ \begin{array}{l}{x_Q} = {x_T} = - OD = - \left( {AD - OA} \right) = - 6\\{y_Q} = {y_T} = OH = \frac{{AB}}{2} = 3\end{array} \right.\).
\({z_Q} = QT = 7\)
Suy ra \(Q\left( { - 6;\,3;\,7} \right)\).
b) Đúng. Vì \(C \in \left( {Oxy} \right)\) nên \({z_C} = 0\).
Ta có \(\left\{ \begin{array}{l}{x_C} = - OD = - 6\\{y_C} = ON = AB = 6\end{array} \right.\).Suy ra \(C\left( { - 6;\,6;\,0} \right)\).Vậy \(\overrightarrow {OC} = \left( { - 6;\,6;\,0} \right)\).
c) Đúng Gọi \(L\) là trung điểm của \(FG\).
Ta có: \({z_K} = OK = AE = 5\).
Suy ra \(K\left( {0;\,0;\,5} \right)\).
\( \Rightarrow OK = 5\).
\(B\), \(C\) lần lượt là hình chiếu của \(F\), \(G\) lên \(\left( {Oxy} \right)\).
Suy ra \(F\left( {2;\,6;\,5} \right)\), \(G\left( { - 6;\,6;\,5} \right)\).
Mà \(L\) là trung điểm của \(FG\) nên \(L\left( { - 2;\,6;\,5} \right)\)\( \Rightarrow KL = 2\sqrt {10} \).
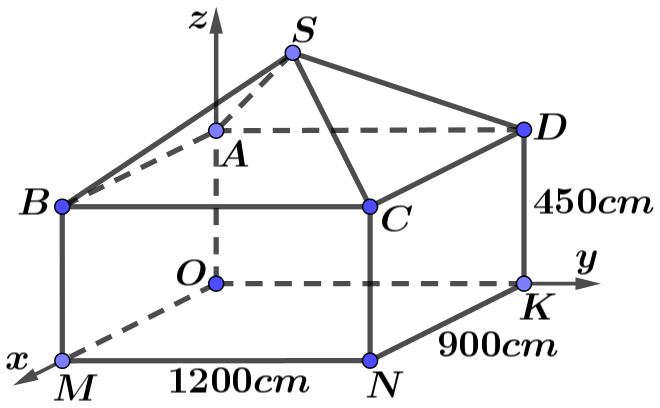
Vậy độ dài đoạn cáp tối thiểu từ \(O\) đến \(K\)sau đó nối thẳng đến camera là
\(OK + KL = 5 + 2\sqrt {10} \) (m)
d) Sai.\(FG = \sqrt {{{\left( { - 6 - 2} \right)}^2} + {{\left( {6 - 6} \right)}^2} + {{\left( {5 - 5} \right)}^2}} = 8\) (m) .
\(GQ = \sqrt {{{\left( { - 6 + 6} \right)}^2} + {{\left( {3 - 6} \right)}^2} + {{\left( {7 - 5} \right)}^2}} = \sqrt {13} \) (m).
Suy ra \({S_{FGQP}} = FG \cdot GQ = 8\sqrt {13} \)\(\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Diện tích lợp tôn mái nhà là \(2{S_{FGQP}} = 16\sqrt {13} \)\(\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Số tiền cần bỏ ra để mua tôn lợp mái nhà là
\(16\sqrt {13} \cdot 130\,000 \approx 7\,500\,000\) (đồng).
Câu 3
\(\alpha = 90^\circ \).
\(\alpha = 180^\circ \).
\(\alpha = 60^\circ \).
\(\alpha = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.