Dạng 3. Trắc nghiệm trả lời ngắn
Một chiếc máy đo đạc trắc địa được đặt trên một giá đỡ ba chân. Trọng lực tác dụng lên chiếc máy có độ lớn là \(30{\rm{N}}\) và được phân bố thành ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) lên ba chân của giá đỡ. Ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) có độ lớn bằng nhau và góc tạo bởi mỗi chân của giá đỡ và mặt đất là \(60^\circ .\) Hỏi độ lớn của lực \(\overrightarrow {{F_1}} \) là bao nhiêu Newton (làm tròn đến hàng phần chục)?
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Cánh diều Chương 2 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
11,5
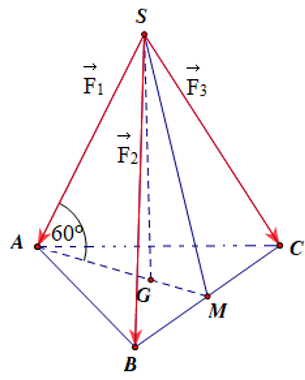
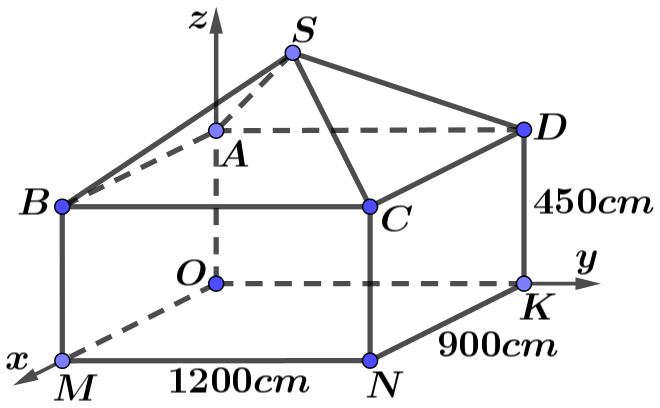
Gán các lực \[\overrightarrow {{F_1}} = \overrightarrow {SA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {SB} ,\,\,\overrightarrow {{F_3}} = \overrightarrow {SC} .\]
Vì \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) và góc tạo bởi mỗi chân của giá đỡ với mặt đất bằng \(60^\circ \) nên \(S.ABC\) là hình chóp đều.
Gọi \(M\) là trung điểm \(BC,\,\,G\) là trọng tâm \(\Delta ABC \Rightarrow SG \bot \left( {ABC} \right).\)
Ta có \(\widehat {SBG} = 60^\circ \Rightarrow SG = SA.\sin 60^\circ = \frac{{SA\sqrt 3 }}{2} \Rightarrow SA = \frac{{2SG}}{{\sqrt 3 }}.\)
Đặt \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} \Rightarrow \left| {\overrightarrow F } \right| = 30\left( {\rm{N}} \right).\)
Vì \(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} = 3\overrightarrow {SG} \Rightarrow \left| {\overrightarrow F } \right| = 3\left| {\overrightarrow {SG} } \right| \Rightarrow SG = \frac{{\left| {\overrightarrow F } \right|}}{3} = 10.\)
Vậy \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {SA} } \right| = 2\frac{{SG}}{{\sqrt 3 }} = \frac{{20}}{{\sqrt 3 }} \approx 11,5\left( {\rm{N}} \right).\)
Đáp án:11,5.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
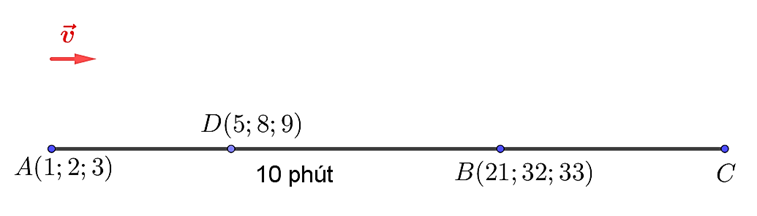
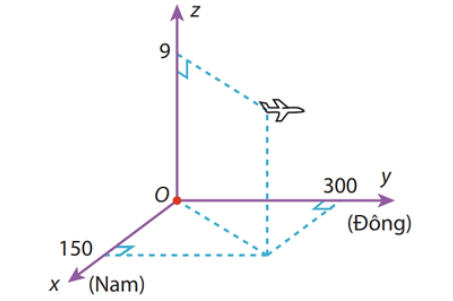
a) Sai.\(\overrightarrow {AB} = \left( {20;\,30;\,30} \right)\); \(\overrightarrow {AD} = \left( {4;\,6;\,6} \right)\).
Ta có \(\frac{{20}}{4} = \frac{{30}}{6} = \frac{{30}}{6}\).
Suy ra \(\overrightarrow {AB} \), \(\overrightarrow {AD} \) cùng phương.
\( \Rightarrow \) 3 điểm \(A\), \(B\), \(D\) thẳng hàng.
Do đó flycam bay qua vị trí \[D\left( {5;\,8;\,9} \right)\].
b) Sai.Flycam ở vị trí \(A\left( {1;\,2;\,3} \right)\) và sau 10 phút nó ở vị trí \(B\left( {21;\,32;\,33} \right)\).
\( \Rightarrow \)\(\overrightarrow {AB} = 10\overrightarrow v \)\( \Leftrightarrow \overrightarrow v = \frac{{\overrightarrow {AB} }}{{10}} = \left( {2;\,3;\,3} \right)\).
c) Đúng. Độ lớn của vận tốc flycam là \(\left| {\overrightarrow v } \right| = \sqrt {{2^2} + {3^2} + {3^2}} = \sqrt {22} \)(m/phút).
d) Đúng.Tại thời điểm \(t = 0\), flycam ở vị trí \(A\) và sau 15 phút flycam ở vị trí \(C\).
Suy ra \(\overrightarrow {AC} = 15\overrightarrow v \)\( \Leftrightarrow \left( {{x_C} - 1;\,{y_C} - 2;\,{z_C} - 3} \right) = 15\left( {2;\,3;\,3} \right)\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 31\\{y_C} = 47\\{z_C} = 48\end{array} \right.\).
Vậy \(C\left( {31;\,47;\,48} \right)\).
Lời giải
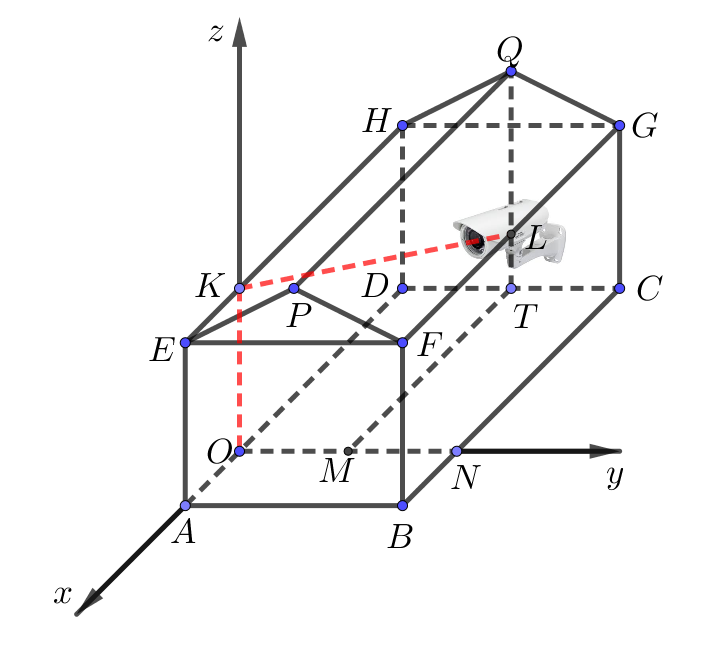
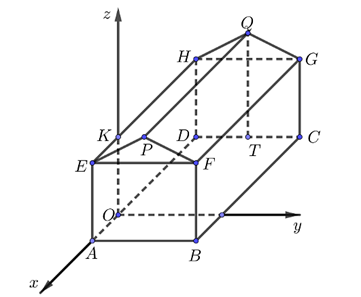
a) Sai. Kẻ \(TM \bot Oy\), \(CN \bot Oy\).
Vì \(T\) là hình chiếu của \(Q\) lên \(\left( {Oxy} \right)\) nên
\(\left\{ \begin{array}{l}{x_Q} = {x_T} = - OD = - \left( {AD - OA} \right) = - 6\\{y_Q} = {y_T} = OH = \frac{{AB}}{2} = 3\end{array} \right.\).
\({z_Q} = QT = 7\)
Suy ra \(Q\left( { - 6;\,3;\,7} \right)\).
b) Đúng. Vì \(C \in \left( {Oxy} \right)\) nên \({z_C} = 0\).
Ta có \(\left\{ \begin{array}{l}{x_C} = - OD = - 6\\{y_C} = ON = AB = 6\end{array} \right.\).Suy ra \(C\left( { - 6;\,6;\,0} \right)\).Vậy \(\overrightarrow {OC} = \left( { - 6;\,6;\,0} \right)\).
c) Đúng Gọi \(L\) là trung điểm của \(FG\).
Ta có: \({z_K} = OK = AE = 5\).
Suy ra \(K\left( {0;\,0;\,5} \right)\).
\( \Rightarrow OK = 5\).
\(B\), \(C\) lần lượt là hình chiếu của \(F\), \(G\) lên \(\left( {Oxy} \right)\).
Suy ra \(F\left( {2;\,6;\,5} \right)\), \(G\left( { - 6;\,6;\,5} \right)\).
Mà \(L\) là trung điểm của \(FG\) nên \(L\left( { - 2;\,6;\,5} \right)\)\( \Rightarrow KL = 2\sqrt {10} \).
Vậy độ dài đoạn cáp tối thiểu từ \(O\) đến \(K\)sau đó nối thẳng đến camera là
\(OK + KL = 5 + 2\sqrt {10} \) (m)
d) Sai.\(FG = \sqrt {{{\left( { - 6 - 2} \right)}^2} + {{\left( {6 - 6} \right)}^2} + {{\left( {5 - 5} \right)}^2}} = 8\) (m) .
\(GQ = \sqrt {{{\left( { - 6 + 6} \right)}^2} + {{\left( {3 - 6} \right)}^2} + {{\left( {7 - 5} \right)}^2}} = \sqrt {13} \) (m).
Suy ra \({S_{FGQP}} = FG \cdot GQ = 8\sqrt {13} \)\(\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Diện tích lợp tôn mái nhà là \(2{S_{FGQP}} = 16\sqrt {13} \)\(\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Số tiền cần bỏ ra để mua tôn lợp mái nhà là
\(16\sqrt {13} \cdot 130\,000 \approx 7\,500\,000\) (đồng).
Câu 3
\(\alpha = 90^\circ \).
\(\alpha = 180^\circ \).
\(\alpha = 60^\circ \).
\(\alpha = 45^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập