Dạng 2. Trắc nghiệm đúng sai
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Trong không gian với hệ trục tọa độ \(Oxyz\) (đơn vị trên mỗi trục là mét), một ngọn hải đăng được đặt ở vị trí \(I\left( {10;\,\,20;\,\,30} \right)\) với bán kính phủ sáng là \(3\)km.
( a) Phương trình mặt cầu mô tả ranh giới bên ngoài của vùng phủ sáng trên biển của hải đăng là
\({\left( {x - 10} \right)^2} + {\left( {y - 20} \right)^2} + {\left( {z - 30} \right)^2} = {3000^2}\).
(b) Người đi biển ở vị trí \(A\left( {50;20;0} \right)\) nhìn thấy được ánh sáng của ngọn hải đăng.
(c) Người đi biển ở vị trí \(B\left( {4030;\,\,50;\,\,40} \right)\) nhìn thấy được ánh sáng của ngọn hải đăng.
(d) Nếu hai người đi biển có thể nhìn thấy ánh sáng của ngọn hải đăng thì khoảng cách giữa hai người đó không quá \(6\)km.
Câu hỏi trong đề: Bài tập ôn tập Toán 12 Cánh diều Chương 5 có đáp án !!
Quảng cáo
Trả lời:
Đáp án:
a) Đúng. Mặt cầu \(\left( S \right)\) tâm \(I\left( {10;\,\,20;\,\,30} \right)\), bán kính \(R = 3\)km = \(3000\)m có phương trình
\({\left( {x - 10} \right)^2} + {\left( {y - 20} \right)^2} + {\left( {z - 30} \right)^2} = {3000^2}\).
b) Đúng. Ta có \(\overrightarrow {IA} = \left( {40;\,0;\, - 30} \right) \Rightarrow IA = \sqrt {{{40}^2} + {0^2} + {{30}^2}} = 50\,{\rm{m}} < \,R = 3000\,{\rm{m}}\)nên điểm \(A\) nằm trong mặt cầu \(\left( S \right)\) nên người đi biển ở vị trí \(A\left( {50;20;0} \right)\) nhìn thấy được ánh sáng của ngọn hải đăng.
c) Sai. Ta có \(\overrightarrow {IB} = \left( {4020;\,30;\,10} \right) \Rightarrow IB = \sqrt {{{4020}^2} + {{30}^2} + {{10}^2}} \approx 4020,12\,{\rm{m}} > R = 3000\,{\rm{m}}\)nên điểm \(B\) nằm ngoài mặt cầu \(\left( S \right)\) nên người đi biển ở vị trí \(B\left( {4030;\,\,50;\,\,40} \right)\) không nhìn thấy được ánh sáng của ngọn hải đăng.
d) Đúng. Vì bán kính phủ sáng là \(3\)km nên đường kính phủ sáng là \(6\)km nên nếu hai người đi biển có thể nhìn thấy ánh sáng của ngọn hải đăng thì hai người đó nằm trong mặt cầu, do đó khoảng cách giữa hai người đó không quá \(6\)km.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
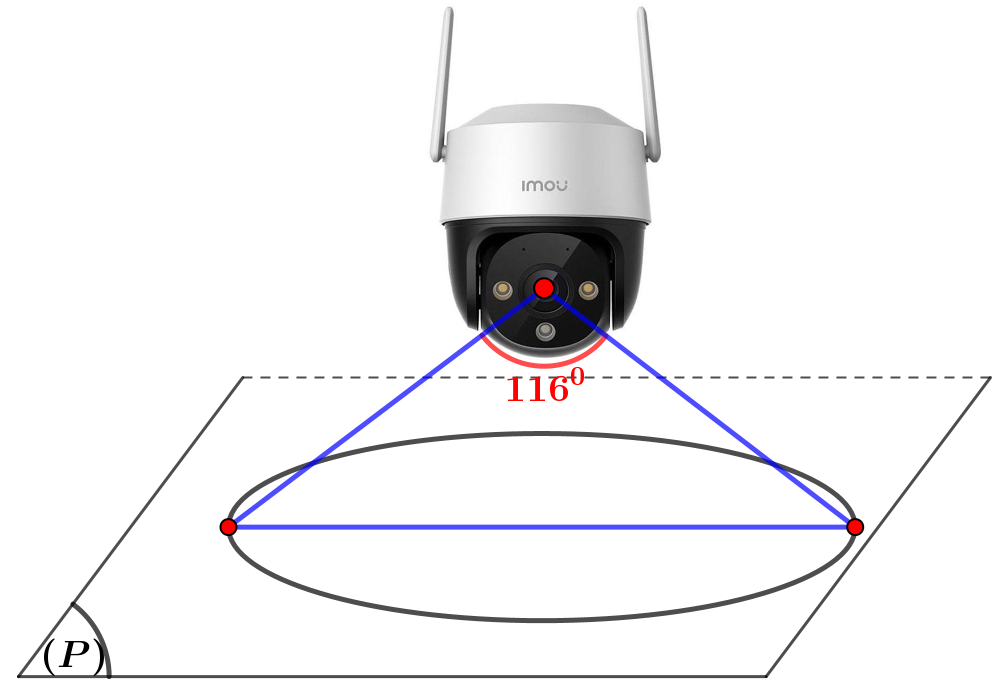
Gọi \(A,B,C\) là các điểm như hình vẽ bên dưới và \(H\) là hình chiếu vuông góc của \(A\) lên mặt phẳng \(\left( P \right)\).
Hình vẽ minh hoạ
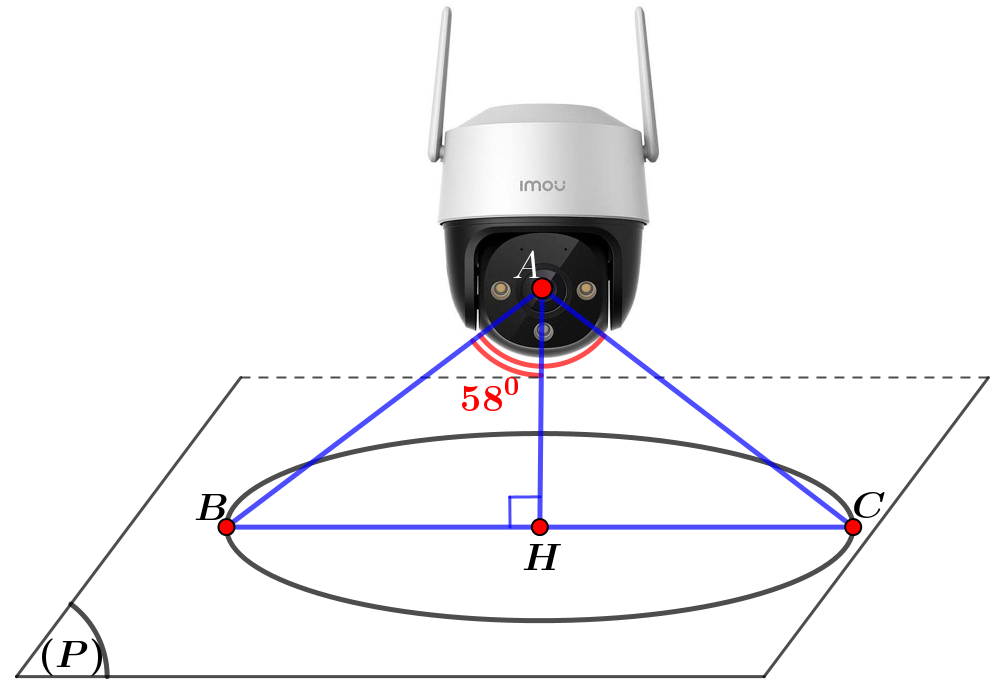
Theo đề \(\widehat {BAC} = 116^\circ \Rightarrow \widehat {BAH} = 58^\circ \). Khi đó \(AH = {\rm{d}}\left( {A,\left( P \right)} \right) = \frac{{\left| {2 \cdot 2 - 1 - 2 \cdot 5 + 13} \right|}}{{\sqrt {4 + 1 + 4} }} = 2\) (đvđd).
Xét tam giác \(ABH\) vuông tại \(H\), ta có: \(\tan \widehat {BAH} = \frac{{BH}}{{AH}} \Rightarrow BH = \tan 58^\circ \cdot 2 = 2\tan 58^\circ \) (đvđd).
Suy ra \(BC = 2BH = 2 \cdot 2\tan 58^\circ \approx 6,4\)(đvđd).
Vậy vùng quan sát của camera trên mặt phẳng \(\left( P \right)\) là hình tròn có đường kính khoảng \(6,4\) (đvđd).
Đáp án: 6,4.
Lời giải
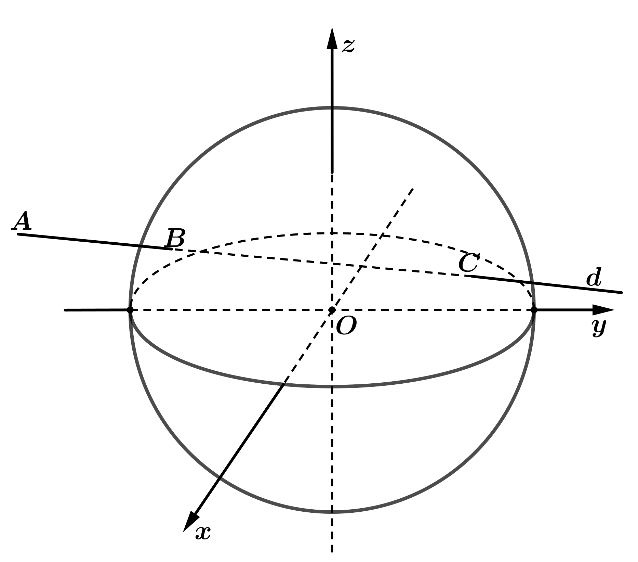
a) Sai. Vì đài kiểm soát không lưu của một sân bay ở vị trí \(O\left( {0;0;0} \right)\) và được thiết kế phát hiện máy bay ở khoảng cách tối đa \(600\)km nên ranh giới vùng phát sóng của đài kiểm soát không lưu trong không gian là mặt cầu có bán kính bằng \(600\)km.
b) Đúng. Ranh giới vùng phát sóng của đài kiểm soát không lưu trong không gian là mặt cầu tâm \(O\left( {0\,;\,0\,;\,0} \right)\) có bán kính bằng \(R = 600\,\)có phương trình là: \({x^2} + {y^2} + {z^2} = 360000\).
c) Đúng. Ta có \(OM = \sqrt {{{\left( { - 500} \right)}^2} + {{\left( {100} \right)}^2} + {{\left( {100\sqrt {11} } \right)}^2}} \approx 608 > 600 = R\).
Vậy, tại vị trí điểm \(M\left( { - 500\,;\,100\,;\,100\sqrt {11} } \right)\) máy bay nằm ngoài vùng kiểm soát không không lưu của đài kiểm soát không lưu sân bay.
d) Sai. Thay \[d:\left\{ \begin{array}{l}x = - 1000 + 100t\\y = - 300 + 80t\\z = 100\sqrt {11} \end{array} \right.\left( {t \in \mathbb{R}} \right)\] vào phương trình mặt cầu \({x^2} + {y^2} + {z^2} = 360000\):
\(\begin{array}{l}{\left( {100t - 1000} \right)^2} + {\left( {80t - 300} \right)^2} + {\left( {100\sqrt {11} } \right)^2} = 360000\\ \Leftrightarrow 164{t^2} - 2480t + 8400 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 10 \Rightarrow B\left( {0\,;\,500\,;\,100\sqrt {11} } \right)\\t = \frac{{210}}{{41}} \Rightarrow C\left( { - \frac{{20000}}{{41}}\,;\,\frac{{4500}}{{41}}\,;\,100\sqrt {11} } \right)\end{array} \right.\end{array}\)
Quãng đường máy bay di chuyển trong vùng kiểm soát không lưu là:
\(BC = \sqrt {{{\left( { - \frac{{20000}}{{41}}} \right)}^2} + {{\left( {\frac{{4500}}{{41}} - 500} \right)}^2} + {{\left( {100\sqrt {11} - 100\sqrt {11} } \right)}^2}} \approx 625\,\)km.
Vậy thời gian máy bay di chuyển theo đường thẳng \(d\) và trong phạm vi kiểm soát không lưu của sân bay là: \(\frac{{625}}{{900}} = \frac{{25}}{{36}}\) giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.