Nhân dịp đi dã ngoại, lớp 12A dự kiến dựng một cái trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 5 mét, đỉnh trại cách nền 3 mét. Thể tích phần không gian bên trong lều trại bằng bao nhiêu mét khối?
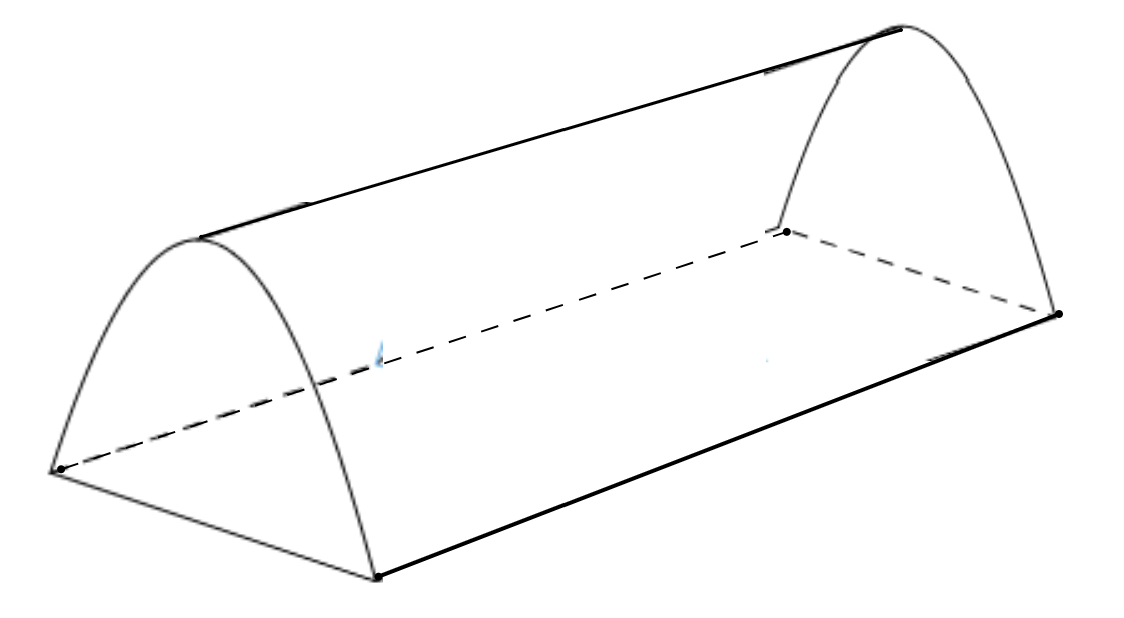
Nhân dịp đi dã ngoại, lớp 12A dự kiến dựng một cái trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 5 mét, đỉnh trại cách nền 3 mét. Thể tích phần không gian bên trong lều trại bằng bao nhiêu mét khối?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn hệ trục tọa độ như hình vẽ, hình dạng khung trại là parabol có phương trình \(y = f\left( x \right) = a{x^2} + bx + c\), vì đỉnh trại cao 3m và bề ngang rộng 3m nên parabol đi qua điểm \(\left( {0;3} \right)\) và \(\left( {\frac{3}{2};0} \right)\).
Ta có : \[\left\{ \begin{array}{l}b = 0\\3 = c\\0 = a.{\left( {\frac{3}{2}} \right)^2} + c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 0\\a = - \frac{4}{3}\\c = 3\end{array} \right.\]
Suy ra parabol có phương trình \(y = f\left( x \right) = - \frac{4}{3}{x^2} + 3\).
Mỗi mặt phẳng vuông góc \[Ox\] tại điểm có hoành độ \[x,\,0 \le x \le h\] cắt khối chóp theo mặt cắt là hình chữ nhật có độ dài các cạnh lần lượt là \[5\] và \[\,\left| {f\left( x \right)} \right|\], có diện tích \(S\left( x \right) = 5.\left| {f\left( x \right)} \right|\) , với \( - \frac{3}{2} \le x \le \frac{3}{2}\).
Vậy thể tích phần không gian trong trại là \(V = \int_{ - \frac{3}{2}}^{\frac{3}{2}} {5.\left| {f\left( x \right)} \right|} dx = 5.\int_{ - \frac{3}{2}}^{\frac{3}{2}} {\left| { - \frac{4}{3}{x^2} + 3} \right|dx = 30\,\,\,{m^3}} \).
Trả lời: 30.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Khi ô tô dừng hẳn thì \(v(t) = 30 - 3t = 0 \Leftrightarrow t = 10\).
Quãng đường ô tô di chuyển được là \(s = \int\limits_0^{10} {\left( {30 - 3t} \right)dt} = \left. {\left( {30t - \frac{{3{t^2}}}{2}} \right)} \right|_0^{10} = 150\)m.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn B
Thể tích của vật thể \(V = \int\limits_{ - 1}^1 {{{\left( {3x} \right)}^2}dx} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \(\mathbb{R}\) và \(\int\limits_1^3 {f(x)dx = } 10\).
a) \(F'(x) = f(x),\forall x \in \mathbb{R}.\)
b) \(F(3) + F(1) = 10\).
c) \(\int\limits_{}^{} {f(x)} dx = F(x) + C\), với C là một hằng số.
d) \(\int\limits_1^3 {(x + f(x))} dx = 14.\)
PHẦN II. TRẮC NGHIỆM ĐÚNG – SAI
Cho hàm số \(F(x)\) là một nguyên hàm của hàm số \(f(x)\) trên \(\mathbb{R}\) và \(\int\limits_1^3 {f(x)dx = } 10\).
a) \(F'(x) = f(x),\forall x \in \mathbb{R}.\)
b) \(F(3) + F(1) = 10\).
c) \(\int\limits_{}^{} {f(x)} dx = F(x) + C\), với C là một hằng số.
d) \(\int\limits_1^3 {(x + f(x))} dx = 14.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập