Cho tam giác \(A\) có đường cao \(AH\) như hình vẽ.
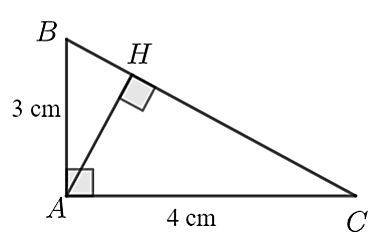
Khẳng định nào đúng?
Cho tam giác \(A\) có đường cao \(AH\) như hình vẽ.

Khẳng định nào đúng?
A. \(\cot \widehat {CAH} = \frac{3}{4}.\)
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có \(\widehat {CAH} = \widehat {CAB}\) (cùng phụ với \(\widehat {BAH}\))
Xét \(\Delta BAC\) vuông tại \(A\) có \(\cot \widehat {ABC} = \frac{{AB}}{{AC}} = \frac{3}{4}\).
Suy ra \(\cot \widehat {ACH} = \frac{3}{4}\).
Vậy chọn đáp án A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
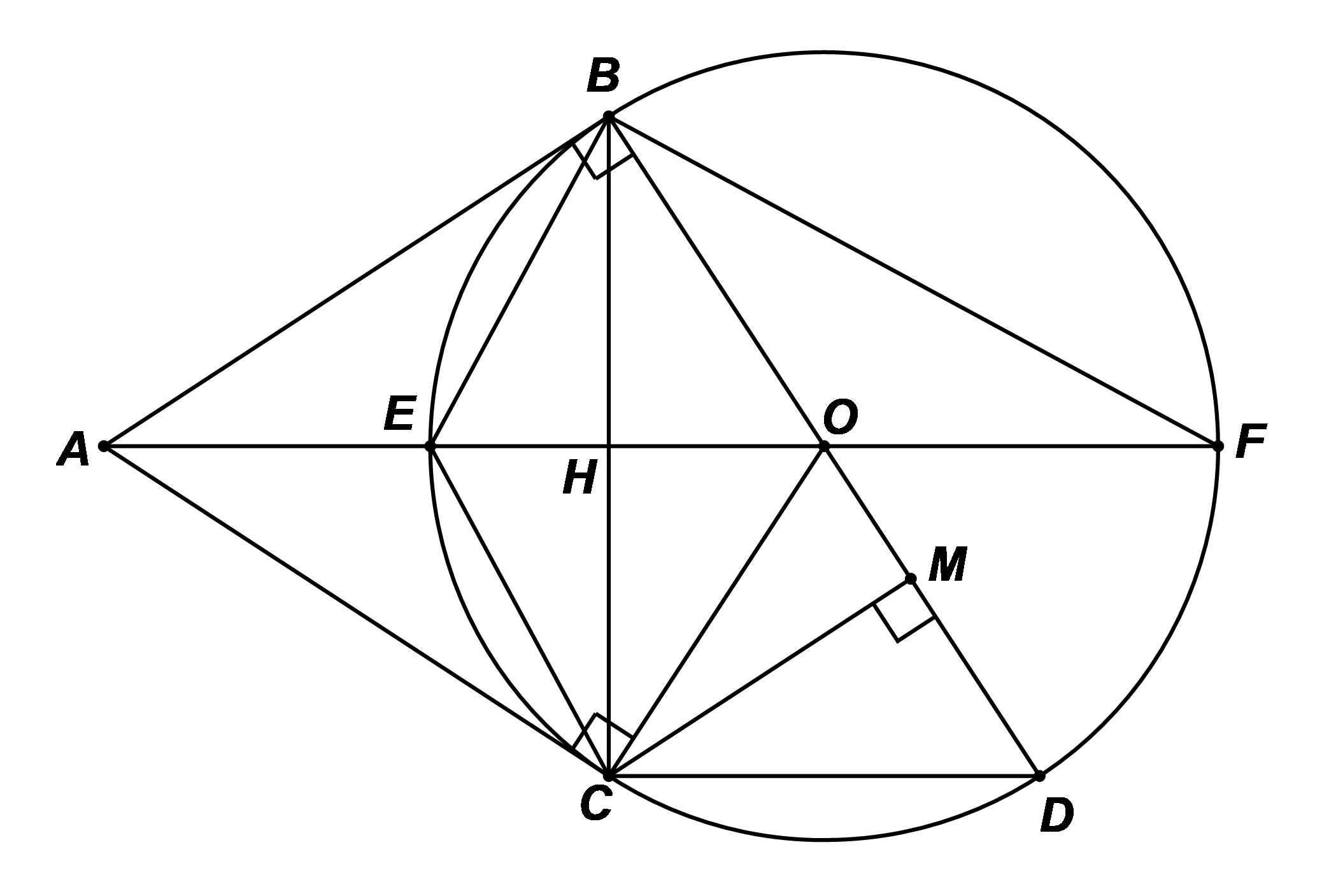
a) Ta có: \(AB,AC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\), suy ra \(OA\) là đường phân giác của \(\widehat {BOC}\) (tính chất) nên \(\widehat {AOC} = \frac{1}{2}\widehat {BOC}.\)
Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {CDB} = \frac{1}{2}\widehat {BOC}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(BC\))
Do đó, \(\widehat {AOC} = \widehat {CDB}\).
Xét \(\Delta CMD\) và \(\Delta ACO\) có:
\(\widehat {CMD} = \widehat {ACO} = 90^\circ \) và \(\widehat {CDM} = \widehat {AOC}\) (do \(\widehat {AOC} = \widehat {CDB}\))
Do đó (g.g).
b) Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {EBF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Ta có \(\widehat {ABO} = \widehat {EBF} = 90^\circ \) nên \(\widehat {ABE} + \widehat {EBO} = \widehat {EBO} + \widehat {OBF}\)
Suy ra \(\widehat {ABE} = \widehat {OBF}\).
Lại có: \(\widehat {OBF} = \widehat {OFB}\) (vì \(\Delta BOF\) cân tại \(O\) do \(OB = OF)\) suy ra \(\widehat {ABE} = \widehat {OFB}\) (1)
Mà \(\widehat {ECB} = \widehat {OFB}\) (hai góc nội tiếp cùng chắn cung \(EC\) của đường tròn tâm \(O\)) (2)
Từ (1) và (2) suy ra \(\widehat {ECB} = \widehat {ABE}\). (3)
Mặt khác, \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau) và \(OB = OC = R\)
Suy ra \(OA\) là đường trung trực của \(BC\) mà \(E \in OA\), suy ra \(EB = EC\).
Do đó \(\Delta EBC\) cân tại \(E\) nên \(\widehat {ECB} = \widehat {EBC}\). (4)
Từ (3) và (4) suy ra \(\widehat {EBC} = \widehat {ABE}\) nên \(BE\) là tia phân giác của góc \(B\) trong tam giác \(ABH\).
Vậy \[BE\] là phân giác của \(\widehat {ABC}.\)
c) Theo câu a, (g.g), suy ra \(\widehat {OAC} = \widehat {DCM} = 30^\circ \).
Suy ra \(\widehat {AOC} = 90^\circ - \widehat {OAC} = 90^\circ - 30^\circ = 60^\circ \).
Do đó, \(\widehat {BOC} = 2\widehat {AOC} = 120^\circ \) hay
Xét \(\Delta AHC\) vuông tại \(H\), có: \(\cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
Suy ra \(AC = \frac{{AH}}{{\cos \widehat {HAC}}} = \frac{4}{{\cos 30^\circ }} = \frac{{8\sqrt 3 }}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)
Xét \(\Delta AOC\) vuông tại \(C\), có: \(OC = AC.\tan \widehat {OAC} = \frac{{8\sqrt 3 }}{3}.\tan 30^\circ = \frac{8}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)
Diện tích hình quạt giới hạn bởi các bán kính \[OB,OC\] và cung nhỏ \(BC\) là:
\[S = \frac{{\pi .{{\left( {\frac{8}{3}} \right)}^2} \cdot 120}}{{360}} = \frac{{64\pi }}{{27}}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Đúng. c) Đúng. d) Sai.
• Gọi giá niêm yết của quyển sách bồi dưỡng Toán và quyển sách bồi dưỡng Ngữ Văn lần lượt là \(x,{\rm{ }}y\) (đồng). Điều kiện xác định \(x > 0,{\rm{ }}y > 0.\)
Do đó, ý a) là đúng.
• Vì một quyển sách bồi dưỡng Toán và một quyển sách bồi dưỡng Ngữ Văn với tổng số tiền theo giá niêm yết là \(270{\rm{ }}000\) đồng nên ta có phương trình \(x + y = 270{\rm{ }}000\). Do đó, ý b) là đúng.
• Vì An mua vào lúc cửa hàng có chương trình giảm giá nên khi thanh toán quyển sách Toán được giảm giá \(10\% \); quyển sách Ngữ Văn được giảm giá \(20\% \) nên chỉ cần phải trả \(228{\rm{ }}000\) đồng.
Do đó, ta có \(\left( {100\% - 10\% } \right)x + \left( {100\% - 20\% } \right)y = 228{\rm{ }}000\) hay \(0,9x + 0,8y = 228{\rm{ }}000\).
Từ đây, ta có hệ phương trình \(\left\{ \begin{array}{l}x + y = 270{\rm{ }}000\\0,9x + 0,8y = 228{\rm{ }}000\end{array} \right.\).
Do đó, ý c) là đúng.
• Từ phương trình \(x + y = 270{\rm{ }}000\) suy ra \(y = 270{\rm{ }}000 - x\).
Thay \(y = 270{\rm{ }}000 - x\) vào \(0,9x + 0,8y = 228{\rm{ }}000\) ta được
\(0,9x + 0,8\left( {270{\rm{ }}000 - x} \right) = 228{\rm{ }}000\)
\(0,9x + 0,8 \cdot 270{\rm{ }}000 - 0,8x = 228{\rm{ }}000\)
\(0,1x = 228{\rm{ }}000 - 0,8 \cdot 270{\rm{ }}000\)
\(0,1x = 12{\rm{ }}000\)
\(x = 120{\rm{ }}000\)
Thay \(x = 120{\rm{ }}000\) suy ra \(y = 270{\rm{ }}000 - 120{\rm{ }}000 = 150{\rm{ }}000\) (đồng).
Vậy giá niêm yết của quyển sách bồi dưỡng Toán là \(120{\rm{ }}000\) đồng và quyển sách bồi dưỡng Ngữ Văn là \(150{\rm{ }}000\) đồng.
Vậy ý d) là sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
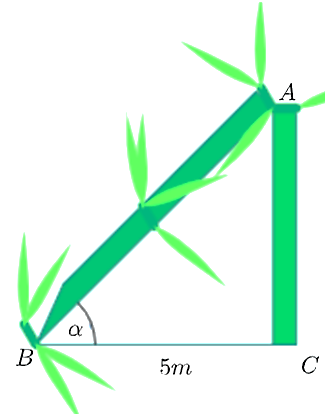
![Bác An có mảnh vườn hình vuông \[ABCD\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/25-1761112465.png)